A Medellín la pioggia🌧️ arriva spesso nel pomeriggio, rapida e densa. L’aria cambia odore: terra bagnata, foglie, un soffio fresco che placa per un attimo il ronzio della città. È in una di queste pause sospese che ho deciso di togliermi una vecchia curiosità: capire fino a che punto le analogie vettoriali funzionino ancora nei modelli di embedding più recenti, come Gemini di Google — ma sarebbe potuto essere anche Ada di OpenAI.

Word Embeddings, tra statico e dinamico

Meaning is something of a holy grail in the study of language
- Magnus Sahlgren

I semantic vectors o word embeddings rappresentano parole, frasi o documenti come vettori in uno spazio multidimensionale. In questo spazio, parole con significati simili si trovano vicine, mentre quelle con significati diversi sono distanti. Questa rappresentazione rende il linguaggio processabile in modo efficiente e trova applicazione in text classification, text generation, machine translation, named entity recognition (NER), information retrieval, recommendation systems e altri ambiti dell’elaborazione del linguaggio naturale.

Semantic vector

Un semantic vector è la rappresentazione matematica di una parola (o di un concetto) come punto in uno spazio multidimensionale. La posizione di ogni vettore dipende dal significato della parola e dalle relazioni statistiche che ha con le altre nel corpus di addestramento. Due parole con significato simile avranno vettori vicini; relazioni specifiche, come uomo → donna o singolare → plurale, corrispondono a direzioni in questo spazio.

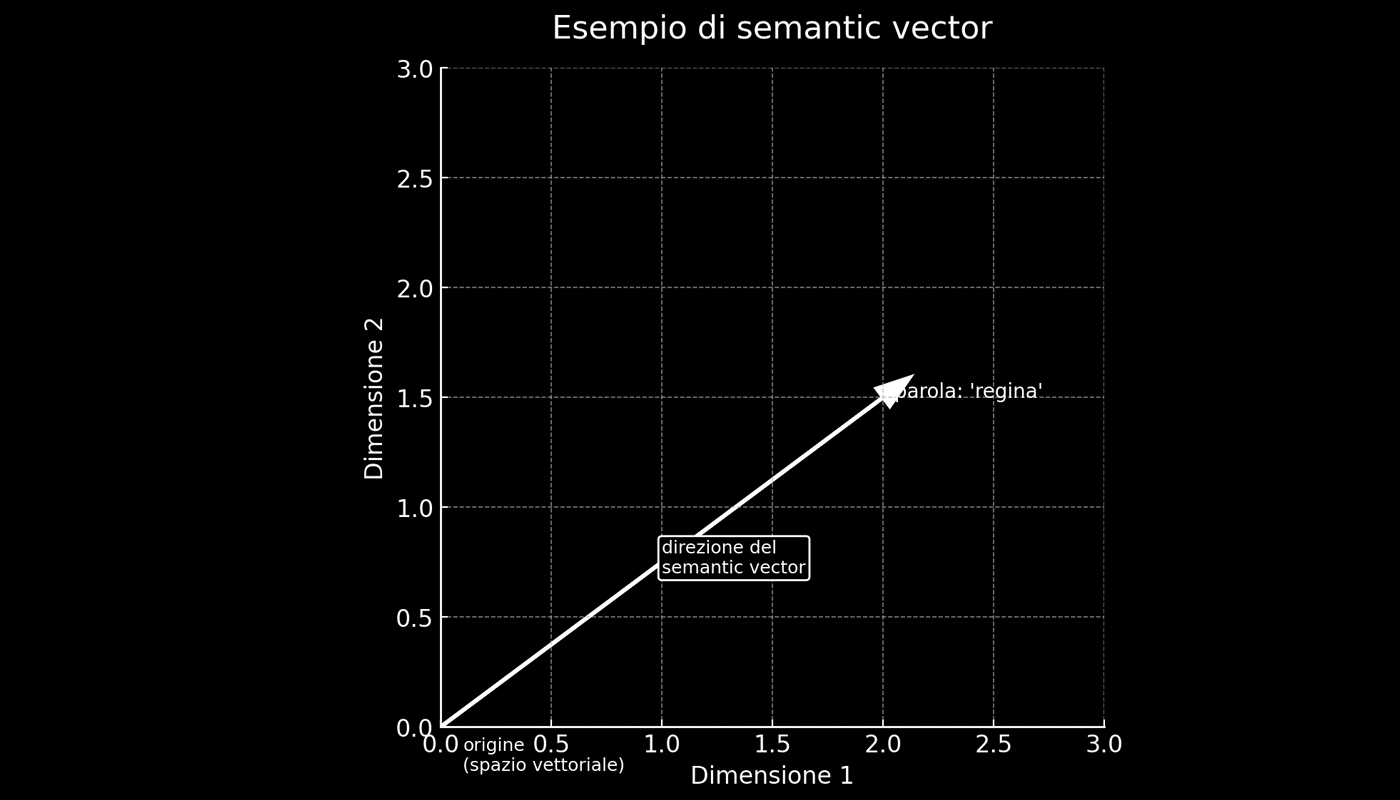
Si parla di static embeddings quando a ogni parola viene assegnato un solo vettore, indipendente dal contesto. Modelli come word2vec e GloVe funzionano così: la parola “banca” avrà la stessa rappresentazione sia nel senso di istituto di credito che di riva del fiume. Con i dynamic embeddings, invece, il vettore cambia a seconda del contesto d’uso. In modelli come ELMo, BERT o GPT, “banca” avrà rappresentazioni diverse se compare in “ho depositato i soldi in banca” oppure in “mi sono seduto sulla banca del fiume”.

Nel 2013, gran parte del successo iniziale nel campo dei word embeddings può essere attribuito a due modelli chiave: GloVe (Global Vectors for Word Representation) e Word2vec (Word to Vector).
GloVe, sviluppato nel 2014 da Jeffrey Pennington, Richard Socher e Christopher D. Manning all’Università di Stanford, generava i vettori basandosi sulla co-occorrenza delle parole.
Word2vec, ideato nel 2013 dal fisico Tomas Mikolov e da un gruppo di ricercatori di Google, utilizzava invece una rete neurale per prevedere il contesto di una parola o completare una parola mancante in una sequenza.

Tra il 2013 e il 2015, la progettazione degli embedding statici era fortemente “geometrica”: lo spazio multidimensionale era concepito quasi come un foglio di carta📄, dove le direzioni dei semantic vectors associate a relazioni come genere, tempo verbale o numero singolare/plurale potevano essere rappresentate come traslazioni lineari costanti. Ad esempio, la direzione che va da uomo ➡️ donna è molto simile a quella da re ➡️ regina. Allo stesso modo, la direzione da correre ➡️ correva è simile a quella da mangiare ➡️mangiava.

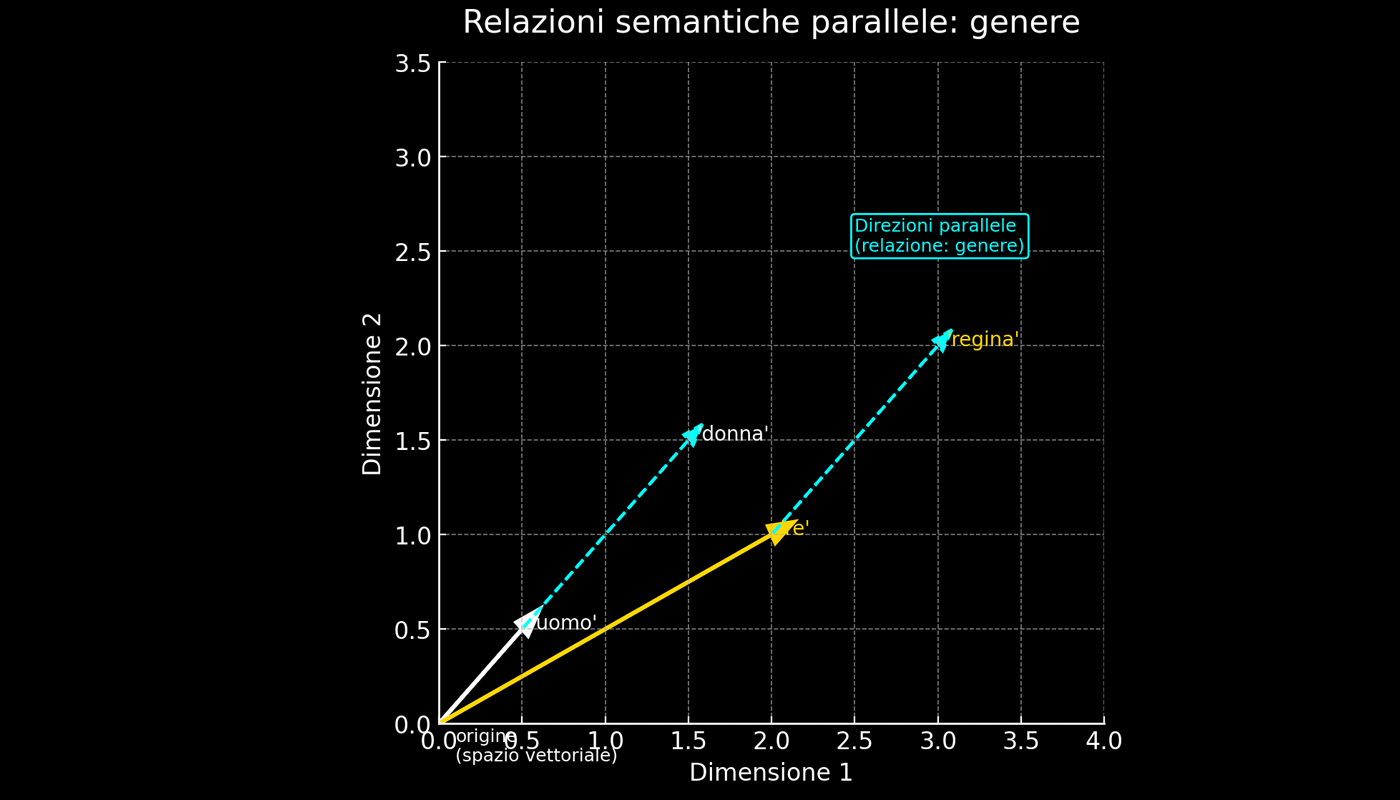
Con Gemini (o gli embedding di GPT-4, OpenAI Ada-002 ecc.), lo spazio appare più simile a un terreno montuoso⛰️: vicino a un punto la direzione “genere” è ancora riconoscibile, ma spostandosi cambia inclinazione. Per questo alcune analogie funzionano ancora (con un buon ranking), ma la linearità perfetta non è più garantita.

Analogie vettoriali

Le analogie vettoriali — o “aritmetica” dei word embeddings — descrivono il fenomeno per cui differenze semantiche ricorrenti si traducono in traslazioni lineari nello spazio dei vettori. Se la relazione maschile → femminile corrisponde a uno spostamento simile per molte coppie (uomo → donna, re → regina, attore → attrice), allora sottrarre “uomo” e sommare “donna” al vettore “re” porta vicino a “regina”.

Nei modelli con embeddings statici, relazioni di questo tipo — come il genere — tendono a essere traslazioni lineari costanti. In altre parole, lo spazio era organizzato come se contenesse veri e propri “assi semantici globali", con orientamento stabile su tutto il vocabolario.

In termini matematici:

$$ \vec{v}_{\text{queen}} \approx \vec{v}_{\text{king}} - \vec{v}_{\text{man}} + \vec{v}_{\text{woman}} $$

Il risultato è vicino a “queen” perché le coppie formano un parallelogramma nello spazio embedding: i lati opposti hanno stessa lunghezza e direzione. Questa regolarità non è "magia", ma emerge dalle statistiche di co-occorrenza delle parole.

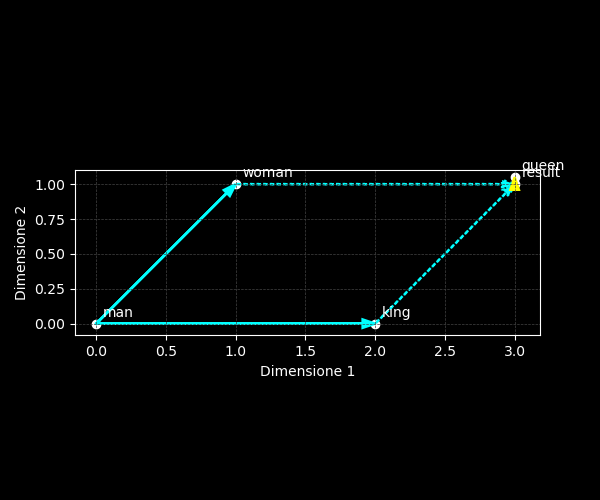
Nei modelli recenti, come Gemini Embedding (o gli embedding di GPT-4, OpenAI Ada-002 e simili), l’addestramento non si basa più soltanto su co-occorrenze o previsioni di parola, ma su obiettivi compositi — spesso supervisionati — pensati per retrieval, search e ranking.

L’input non è più limitato alla singola parola, ma può essere un’intera frase o documento. Questo cambia la geometria dello spazio: le direzioni semantiche non sono più “assi globali” stabili, ma relazioni locali che possono variare a seconda del contesto e del dominio del dato. Di conseguenza, in Gemini “uomo” non ha lo stesso embedding di “un uomo gentile”: la parola viene rappresentata come concetto situato nella frase, e il vettore cambia in base al contesto sintattico e semantico. Questo rompe l’assunto dei modelli statici secondo cui una parola possiede un vettore unico, riutilizzabile per tutte le analogie.

Più che un esperimento una curiosità🧐

Approfittando della tranquillità del rumore della pioggia🌧️ — che per me è quasi un metronomo naturale capace di mantenre il focus della mia attenzione — ho deciso di togliermi una curiosità che avevo da tempo. Invece di usare l’embedding di una singola parola (zio, uomo, donna) come negli embedding classici, ho calcolato l’embedding medio di più definizioni brevi e parallele di ciascun termine, per ridurre la variabilità dovuta al contesto e ottenere vettori più stabili.

Dal vettore medio di zio ho sottratto quello di uomo e aggiunto quello di donna, confrontando il risultato con i vettori medi di altre possibili risposte (zia, cugina, sorella, ecc.) e calcolando la similarità coseno per ottenere un ranking.

Google Gemini Embedding

Il modello Gemini Embedding di Google si distingue per prestazioni elevate su benchmark come MTEB — ad esempio, un punteggio medio di 68,37 nella versione multilingue — e per il supporto di oltre 100 lingue. Utilizza un approccio innovativo, il Matryoshka Representation Learning (MRL)🪆, che ottimizza la rappresentazione mantenendo un’elevata efficienza nell’uso della memoria.

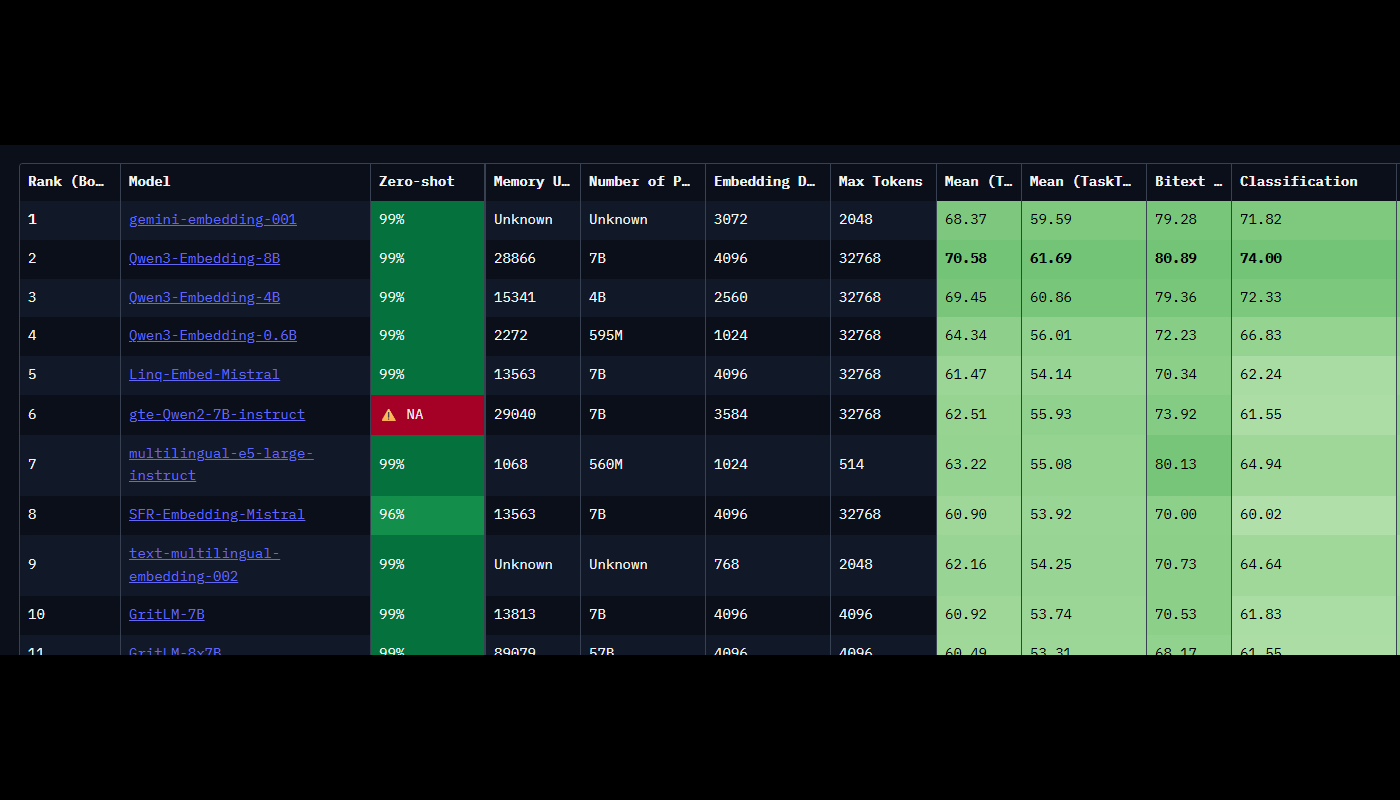
MRL 🪆è una tecnica di representation learning che permette a un singolo embedding di essere utilizzato in dimensioni diverse, come le bambole Matryoshka che si incastrano l’una nell’altra.

Durante l’addestramento, il modello viene ottimizzato contemporaneamente per più versioni troncate dell’embedding, così da concentrare le informazioni più importanti nelle prime dimensioni. Ad esempio, un embedding prodotto a 1024 dimensioni può essere ridotto a 256 dimensioni mantenendo gran parte delle informazioni utili: in un sistema di ricerca semantica su milioni di documenti, questo consente di ridurre di quattro volte lo spazio su disco e velocizzare la ricerca, mentre per il reranking finale si può tornare a usare l’embedding completo da 1024 dimensioni per massimizzare la precisione.

Tinkerando con la spazio multidimensionale

Dando un’occhiata all’articolo “Gemini Embedding now generally available in the Gemini API” di Google, scopriamo che Gemini Embedding gestisce fino a 2.048 token in input e produce vettori fino a 3.072 dimensioni, raddoppiando così la capacità degli embedding precedenti.

Dimensionalità

Ora, cerchiamo di comprendere la dimensionalità del nostro vettore di embedding. Se sei a tuo agio con lo spazio tridimensionale (le classiche X, Y e Z), immagina che questo vettore si estenda in uno spazio di ben 3.072 dimensioni: un concetto quasi impossibile da visualizzare per noi esseri umani.

from google import genai

client = genai.Client(api_key="")

result = client.models.embed_content(
    model="gemini-embedding-001",
    contents="Che cos'è il significato della vita?"
)

embedding_obj = result.embeddings[0]

# Prendi la lista di float
values = embedding_obj.values

# Conta quanti valori ci sono
print(len(values)) # Di default: 3072 dimensioni
print(values[:5])   # Prime 5 componenti del vettore

Una dimensionalità così alta consente di codificare una grande quantità di informazioni semantiche e sintattiche, rappresentando sfumature di significato che in spazi meno complessi andrebbero perse.

Proprietà spaziali

Abbiamo già visto come lo studio del linguaggio, nell’ambito del NLP moderno, si può tradurre in un problema di geometria nello spazio vettoriale. In questo spazio, una delle proprietà più interessanti è che l’addizione e la sottrazione di vettori semantici producono a loro volta un nuovo vettore, ancora interpretabile linguisticamente.

Un modo efficace per comprenderlo è “tinkerare” con i vettori. Prima si ottiene una rappresentazione numerica per ogni parola o concetto, poi si sperimentano operazioni aritmetiche per esplorare analogie e trasformazioni di significato.

Nel nostro esempio il metodo emb() produce embedding semantici ad alta dimensionalità a partire da una singola frase, mentre emb_mean() calcola la media degli embedding di più frasi parallele legate allo stesso concetto. Questa media riduce la variabilità introdotta dalle diverse formulazioni testuali e restituisce un vettore più stabile e rappresentativo del significato complessivo.

def emb(txt: str) -> np.ndarray:
	"""
	Estrazione del vettore di embedding dalla risposta dell'API
	e conversione in array NumPy float64.
	:param txt:
	:return:
	"""
	r = client.models.embed_content(model="gemini-embedding-001", contents=txt)
	return np.array(r.embeddings[0].values, dtype=np.float64)

def emb_mean(texts: list[str]) -> np.ndarray:
	"""
	Calcola l'embedding per ogni frase in 'texts' e li impila in una matrice (shape: N x D).
	:param texts:
	:return:
	"""
	# Questo riduce la variabilità frase-per-frase e stabilizza il concetto.
	V = np.stack([emb(t) for t in texts], axis=0)
	return V.mean(axis=0)

Un aspetto importante di queste rappresentazioni è la capacità di risolvere analogie di parole della forma “A sta a B ciò che C sta a X” utilizzando l’aritmetica semplice. In pratica l’uomo sta alla donna come lo zio sta a zia, sfruttando un metodo di offset vettoriale che si basa sulla distanza coseno per misurare la somiglianza tra i vettori e trovare il termine più vicino al risultato dell’operazione.

zio – uomo + donna = zia

La similarità coseno confronta l’angolo tra due vettori nello spazio semantico e restituisce un valore compreso tra meno uno e uno, dove uno indica la massima somiglianza possibile

def cos(a, b) -> float:
	"""

	:param a:
	:param b:
	:return:
	"""
	# cosine_similarity si aspetta input 2D: avvolgiamo a e b in liste -> shape (1, D) ciascuno.
	return float(cosine_similarity([a],[b])[0][0])

Per calcolare questa misura utilizziamo la funzione cos(a, b), che prende due vettori in ingresso e li adatta al formato richiesto da cosine_similarity.

La funzione restituisce un singolo numero in virgola mobile che rappresenta il grado di somiglianza tra i due concetti, permettendo così di ordinare i candidati in base alla vicinanza semantica con il risultato dell’analogia.

Definizioni brevi

Adesso anziché utilizzare la singola parola come “zio”, “uomo” o “donna”, come avremmo fatto con i modelli statici di embeddings scegliamo di descrivere ciascun concetto con più frasi brevi e parallele.

# 1) Definizioni brevi (per creare rappresentazioni robuste dei concetti)
zio_defs = [
	"Lo zio è un parente maschio della famiglia.",
	"Lo zio è il fratello del padre o della madre.",
	"Lo zio è un adulto di genere maschile con legame di parentela."
]
uomo_defs = [
	"L'uomo è un adulto di genere maschile.",
	"Un uomo è una persona adulta maschile.",
	"L'uomo è un essere umano maschio adulto."
]
donna_defs = [
	"La donna è un adulto di genere femminile.",
	"Una donna è una persona adulta femminile.",
	"La donna è un essere umano femmina adulta."
]

Ogni frase esprime la stessa idea con parole leggermente diverse, così da dare al modello più contesto e ridurre l’effetto di eventuali ambiguità.

Calcoliamo i vettori medi

Calcolando l’embedding medio di queste frasi, otteniamo una rappresentazione più robusta e stabile, meno influenzata dalla formulazione specifica di una singola frase.

v_zio   = emb_mean(zio_defs)
v_uomo  = emb_mean(uomo_defs)
v_donna = emb_mean(donna_defs)

Questo approccio dovrebbe aiutare il modello a catturare il significato centrale del concetto, migliorando la qualità delle analogie rispetto a quando si usa una sola parola. Adesso possiamo applicarla al risultato dell’operazione zio – uomo + donna per confrontarlo con un insieme di candidati come zia, cugina, sorella, madre e nonno.

Aritmetica dei vettori

Dopo aver ottenuto i vettori medi per “zio”, “uomo” e “donna”, possiamo costruire l’analogia vera e propria tentando di capire se con l’uso di definizioni parallele e l’aritmetica vettoriale sia davvero possibile catturare relazioni semantiche in modo chiaro e misurabile.

Relazioni di genere

Applichiamo la classica operazione zio – uomo + donnasottraendo la componente semantica di “uomo” da “zio” e aggiungendo quella di “donna”, ottenendo un nuovo vettore che dovrebbe avvicinarsi al concetto di “zia”. Così facendo dovremmo spostare il significato dal dominio maschile a quello femminile mantenendo il contesto di partenza.

v_result = v_zio - v_uomo + v_donna

Per verificare se il vettore ottenuto dall’analogia corrisponde davvero al concetto atteso, lo confrontiamo con un insieme di candidati. Anche in questo caso, quando possibile, ogni candidato è descritto attraverso più frasi parallele che ne catturano il significato in modo completo.

# 4) Candidati di confronto, anch'essi con definizioni parallele (quando possibile)
def_defs = {
	"zia": [
		"La zia è una parente femmina della famiglia.",
		"La zia è la sorella del padre o della madre.",
		"La zia è un adulto di genere femminile con legame di parentela."
	],
	"cugina": ["La cugina è una parente femmina della famiglia."],
	"sorella": ["La sorella è la figlia degli stessi genitori, di genere femminile."],
	"madre": ["La madre è il genitore femminile."],
	"nonno": ["Il nonno è il padre del padre o della madre."]
}

La lista include “zia” come opzione più probabile, ma anche termini semanticamente vicini come “cugina”, “sorella” o “madre” e un termine volutamente distante come “nonno”. In questo modo possiamo osservare non solo se il sistema trova la risposta corretta, ma anche come distribuisce le similarità tra concetti affini e non affini.

scores = []
for w, defs in def_defs.items():
	v = emb_mean(defs)
	scores.append((w, cos(v_result, v)))

scores_sorted = sorted(scores, key=lambda x: x[1], reverse=True)
print("Ranking (zio – uomo + donna):")
for w, s in scores_sorted:
	print(f"{w:8s}  {s:.4f}")

Per ogni voce nella lista def_defs otteniamo il vettore medio delle sue definizioni e misuriamo la similarità coseno con v_result. Ogni coppia composta dal termine e dal suo punteggio viene aggiunta a una lista, che poi ordiniamo in ordine decrescente di similarità. Infine stampiamo il ranking, così da vedere quale candidato risulta più vicino all’analogia “zio – uomo + donna” e quanto distano gli altri in termini di significato.

Ranking (zio – uomo + donna):
zia       0.9162
cugina    0.8275
sorella   0.7832
madre     0.7505
nonno     0.6930

Il risultato mostra che “zia” ottiene il punteggio di similarità più alto, pari a 0.9162, confermando che l’operazione zio – uomo + donna ha prodotto un vettore molto vicino al concetto atteso. Subito dopo compaiono “cugina” e “sorella”, termini semanticamente vicini e quindi coerenti con l’area semantica della famiglia femminile. “Madre” ottiene un punteggio leggermente inferiore, mentre “nonno”, l’unico candidato maschile, chiude la classifica con la similarità più bassa.

Relazioni di genere

L'analogia più famosa è sicuramente la seguente:

re – uomo + donna = regina

In altre parole, sommando i vettori associati alle parole  re  e  donna  e sottraendo  uomo  si ottiene il vettore associato a  regina . Questo descrive una relazione di genere.

# Definizioni parallele
re_defs = [
    "Il re è il sovrano maschile di un regno.",
    "Il re è un monarca di genere maschile.",
    "Il re è il capo di stato maschio in una monarchia."
]
uomo_defs = [
    "L'uomo è un adulto di genere maschile.",
    "Un uomo è una persona adulta maschile.",
    "L'uomo è un essere umano maschio adulto."
]
donna_defs = [
    "La donna è un adulto di genere femminile.",
    "Una donna è una persona adulta femminile.",
    "La donna è un essere umano femmina adulta."
]

Definiamo i candidati:

# Candidati con definizioni
def_defs = {
    "regina": [
        "La regina è la sovrana femminile di un regno.",
        "La regina è una monarca di genere femminile.",
        "La regina è il capo di stato donna in una monarchia."
    ],
    "principessa": [
        "La principessa è un membro femminile della famiglia reale.",
        "La principessa è la figlia o parente del sovrano in una monarchia."
    ],
    "imperatrice": [
        "L'imperatrice è la sovrana femminile di un impero.",
        "L'imperatrice è una monarca di genere femminile."
    ],
    "consorte": [
        "La consorte è la moglie del sovrano.",
        "La consorte è la partner femminile del monarca."
    ],
    "donna": [
        "La donna è una persona adulta di genere femminile."
    ],
    "re": [
        "Il re è un monarca maschile."
    ]
}

Il risultato è coerente con l’analogia attesa.

Ranking (re - uomo + donna):
regina       0.9179
re           0.8365
imperatrice  0.8095
principessa  0.7926
consorte     0.7746
donna        0.7605

“Regina” ottiene il punteggio più alto (0.9179), confermando che l’offset vettoriale re – uomo + donna cattura correttamente la relazione maschile/femminile nel contesto di una monarchia. Subito dopo compare “re” con 0.8365, che resta semanticamente vicino per via del dominio condiviso, seguito da “imperatrice”, “principessa” e “consorte”, tutti ruoli femminili legati alla sfera reale. “Donna” chiude la classifica, perché pur essendo semanticamente corretta nella dimensione di genere, è molto più generica e meno legata al contesto monarchico.

Relazioni semantiche e geografiche

Ad esempio, possiamo recuperare parole che hanno relazioni semantiche come Paese-Capitale:

Parigi - Francia + Polonia

Iniziamo come sempre con le definizioni:

# Definizioni parallele per città e paesi
parigi_defs = [
    "Parigi è una città europea e capitale della Francia.",
    "Parigi è la capitale francese e un importante centro culturale.",
    "Parigi è la principale città della Francia."
]
francia_defs = [
    "La Francia è uno stato europeo.",
    "La Francia è un paese dell'Europa con capitale Parigi.",
    "La Francia è una nazione europea."
]
polonia_defs = [
    "La Polonia è uno stato europeo.",
    "La Polonia è un paese dell'Europa con capitale Varsavia.",
    "La Polonia è una nazione europea."
]

Definiamo i candidati:

# Candidati
def_defs = {
    "Varsavia": [
        "Varsavia è la capitale della Polonia.",
        "Varsavia è una città europea e capitale polacca.",
        "Varsavia è la principale città della Polonia."
    ],
    "Cracovia": [
        "Cracovia è una grande città della Polonia.",
        "Cracovia è una città storica polacca."
    ],
    "Parigi": [
        "Parigi è la capitale della Francia."
    ],
    "Francia": [
        "La Francia è uno stato europeo."
    ],
    "Polonia": [
        "La Polonia è uno stato europeo."
    ],
    "Berlino": [
        "Berlino è la capitale della Germania."
    ],
    "Praga": [
        "Praga è la capitale della Repubblica Ceca."
    ]
}

Le analogie geografiche funzionano bene quando il modello cattura la relazione capitale di. Se dovesse emergere cracovia o altre città vicine non dovremmo stupirci, dipende da come gli embedding rappresentano i legami città paese nel nostro set di definizioni.

Ranking (parigi - francia + polonia):
Varsavia   0.8983
Polonia    0.8013
Cracovia   0.7556
Parigi     0.7236
Berlino    0.6959
Praga      0.6933
Francia    0.5818

Il ranking dice che l’analogia funziona. Varsavia è in testa, quindi lo spostamento parigi meno francia più polonia porta davvero verso la capitale polacca. Il fatto che Polonia sia seconda è normale. Il vettore risultato conserva una componente di paese perché nelle definizioni compaiono spesso frasi su stato e capitale. In più città e paese condividono molto contesto, quindi la similarità resta alta anche con il paese.

Relazioni morfologiche e sintattiche 

Adesso testiamo le relazioni sintattiche come il singolare-plurale, facciamo il test singolare-plurale in italiano usando sia l’offset medio “plurale − singolare” sia l’analogia diretta “libri − libro + persona ≈ persone”.

libri − libro + persona ≈ persone

Iniziamo con le definizioni a coppia:

pairs = {
    ("gatto","gatti"): (
        ["Il gatto dorme sul divano.", "Questo gatto gioca con una palla.", "Un gatto salta dalla sedia."],
        ["I gatti dormono sul divano.", "Questi gatti giocano con una palla.", "I gatti saltano dalla sedia."]
    ),
    ("libro","libri"): (
        ["Il libro resta sul tavolo.", "Questo libro racconta una storia.", "Un libro pesa poco."],
        ["I libri restano sul tavolo.", "Questi libri raccontano storie.", "I libri pesano poco."]
    ),
    ("fiore","fiori"): (
        ["Il fiore sboccia in primavera.", "Questo fiore profuma molto."],
        ["I fiori sbocciano in primavera.", "Questi fiori profumano molto."]
    ),
    ("persona","persone"): (
        ["La persona cammina in piazza.", "Questa persona parla al medico."],
        ["Le persone camminano in piazza.", "Queste persone parlano al medico."]
    ),
    ("cane","cani"): (
        ["Il cane corre nel parco."],
        ["I cani corrono nel parco."]
    ),
}

Definiamo i candidati:

# Target: persona -> persone
persona_defs = [
    "La persona è un essere umano considerato singolarmente.",
    "Persona è un sostantivo singolare.",
    "La persona è un individuo."
]
persone_defs = [
    "Le persone sono esseri umani considerati collettivamente.",
    "Persone è un sostantivo plurale.",
    "Le persone sono individui."
]

Sorpresa o forse no, “persona” supera “persone”. Il vettore dell’analogia resta vicino al concetto di partenza perché le definizioni condividono molto lessico tra singolare e plurale e perché l’offset che dovrebbe spingere verso il plurale non è abbastanza netto.

Ranking (direzione media del plurale):
persona    0.9645
persone    0.9287
individui  0.8666
donne      0.7944
uomini     0.7938
gente      0.7863

Ranking (libri - libro + persona):
persona    0.9511
persone    0.8968
individui  0.8363
uomini     0.7587
donne      0.7560
gente      0.7512

Adesso possiamo solo fare supposizioni, per esempio che le definizioni usate condividono molto lessico tra singolare e plurale e introducono etichette metalinguistiche come singolare e plurale. Forse la similarità del coseno premia questa somiglianza complessiva, quindi il vettore resta vicino a “persona” e il modello riconosce prima il concetto base e solo dopo la sua variazione di numero.

Credo che gli embedding contestuali dei modelli moderni privilegino il contesto e tendano a conservare il nucleo semantico della frase, di conseguenza il coseno favorisca la prossimità al significato centrale più della trasformazione morfologica.

Che cosa ho imparato? 🤔

La pioggia è ormai cessata, le strade di Medellín riflettono i neon e le insegne come specchi irregolari.

Le analogie vettoriali funzionano bene quando la relazione è forte e ricorrente. Quelle di genere maschile/femminile o città/capitale restano tra le più stabili e leggibili. Usare più frasi parallele per descrivere lo stesso concetto rende la rappresentazione più robusta, e la media degli embedding aiuta a ridurre la variabilità dovuta alla singola formulazione. La similarità coseno è un buon criterio per ordinare i candidati, ma tende a riflettere il contesto condiviso: se le frasi sono troppo simili, il vettore rimane vicino al concetto di partenza, senza compiere il salto atteso.

🔗Sitografia

[0]  King – Man + Woman = Queen: The Marvelous Mathematics of Computational Linguistics, Mit Technology Review, 17/09/2015

[1] Japneet Singh Chawla, What is GloVe?, Medium, 24/04/2018

[2] Kawin Ethayarajh, Word Embedding Analogies: Understanding King – Man + Woman = Queen, Github Blog, 21/06/2019

[3] Florian Huber, King – Man + Woman = King ?, Medium, 15/07/2019

[4] Mohamed Gharibi, The Magic Behind Embedding Models, Medium, 12/12/2019

[5] Plotly , Understanding Word Embedding Arithmetic: Why there’s no single answer to “King − Man + Woman = ?”, Medium, 8/05/2020

[6] Hicham El Boukkouri, Arithmetic Properties of Word Embeddings, Dataiku, 13/08/2020

[7] Antonio Feregrino , Word2vec ilustrado, Tacos de Datos, 04/09/2020

[8] Sam Partee, Vector Embeddings: From the Basics to Production, Partee, 11/08/2022

[9] Tom Aarsen, Introduction to Matryoshka Embedding Models, HuggingFace, 23/02/2024

[10] Thalles Silva, Matryoshka Representation Learning, Thalles' Blog,23/02/2024