Propina: un piccolo gesto che in Colombia racconta di legge, cultura, disuguaglianza e logica fuzzy

In un ristorante di Medellín, alla fine di un pranzo non indimenticabile ma nemmeno deludente, il cameriere si avvicina con il conto e una domanda familiare: «¿Desea incluir el 10% de propina?». Nella voce c’è cortesia, ma anche attesa.
Il piatto era buono, anche se la bandeja paisa è arrivata tiepida.

Il cameriere gentile, ma visibilmente affaticato. L’ambiente curato, ma la musica era così alta da costringermi a ripetere ogni frase. E allora? Quanto lasciare? O, ancor prima: devo lasciare qualcosa?
Da che punto lasci la propina (tutto dipende)
Mi ritrovo spesso sospeso, come dentro un episodio di Ally McBeal, in bilico tra la realtà e un monologo interiore in slow motion. Davanti a me, un gesto minuscolo ma culturalmente denso: la propina, la mancia.
Un atto semplice solo in apparenza.

Come si fa a decidere con un sì o un no, quando l’esperienza è stata “quasi” buona, “abbastanza” piacevole, “lievemente” deludente? Quando il servizio, il cibo, l’atmosfera — e perfino il volume della musica, così alto da disturbare la conversazione — partecipano tutti, in misura diversa, a costruire il mio giudizio complessivo?
La propina appartiene al regno del dipende. È, come cantano gli Jarabe de Palo, qualcosa che “depende de qué lado lo mires”. In Colombia, dove la propina è tecnicamente volontaria, ma spesso suggerita con tono cortese e occhi stanchi, il confine tra libertà e dovere morale si dissolve come il vapore di una arepa calda.
Ed è proprio per questo che, ogni volta che mi viene chiesta, resto lì. Non perché non sappia quanto lasciare, ma perché sento che la mia risposta non può essere compressa in una cifra netta. È come se una parte di me esitasse, consapevole che in quel momento sto decidendo molto più che un arrotondamento sul conto.
Propina in salsa criolla
Il cameriere, il cuoco, il cassiere: tutti partecipano alla catena invisibile che porta il piatto al tavolo. Ma il sistema, fragile, si regge proprio su ciò che la legge definisce come “liberalità del consumatore”. E così, la propina diventa specchio: riflette disuguaglianze e precarietà, ma anche abitudini, generosità, ruoli sociali.
La normativa colombiana — dalla Ley 1935 alla Circular 007 — regola con attenzione il tema: massimo 10%, visibilità in fattura, obbligo d’informare il cliente. Ma nella pratica quotidiana la regola spesso si spezza, scivola e si reinventa. In località turistiche come Cartagena, le denunce di abusi si moltiplicano: propine duplicate, aggiunte arbitrarie, importi esorbitanti.
Molti amministratori di ristoranti dichiarano apertamente che gran parte dei clienti non lascerebbe nulla. E in un mercato del lavoro dove i salari base rasentano il minimo legale, la propina diventa spesso l’unico modo per integrare un reddito dignitoso.
Monologo interiore
Nel mio monologo interiore — sempre in slow motion, come in Ally McBeal — osservo che il cameriere attende la mia decisione. Il conto include già quel 10% “sugerido”, ma la voce, formale e gentile, mi chiede conferma. È lì che comprendo: la risposta non è (solo) economica. È sociale.
La propina non è solo un riconoscimento al servizio ricevuto, ma rende visibile il rapporto tra cliente e lavoratore, tra chi consuma e chi serve. Ad esempio negli Stati Uniti è obbligatoria, in Giappone è scortese. In Colombia... depende.
Secondo l’etimologia, "propina" deriva dal greco propínein, “bere prima”, un gesto rituale augurale legato all’ospitalità. Ma col tempo, ha assunto il significato di gratificazione per un servizio ben reso.
Oggi, però, dare la mancia non significa solo premiare la qualità di ciò che si è ricevuto. Come nota Michael Lynch, studioso del comportamento del consumatore, molti lasciano la mancia per ottenere approvazione sociale, per evitare il senso di colpa, per sentirsi generosi, o semplicemente per rispettare una norma non scritta.
Nel regno del “dipende”
La legge colombiana è chiara.
Non solo sulla volontarietà della propina, ma anche sulla sua destinazione – esclusivamente al personale coinvolto nella catena del servizio – e sul divieto per i proprietari di trattenerne una parte. Inoltre, il diritto colombiano stabilisce che la propina non costituisce salario, e quindi non può essere considerata base di calcolo per i contributi o trattenute.
Ma al di là della norma, resta la domanda fondamentale: come si traduce tutto questo nella mia realtà quotidiana? E, soprattutto, cosa succede quando si cerca di tradurre tutto questo in codice python?
Logica Fuzzy
La logica fuzzy, introdotta nel 1965 dal matematico Lotfi Zadeh (1921-2017) , nasce proprio per affrontare situazioni come questa: decisioni ambigue, valutazioni qualitative, giudizi non numerici ma sfumati. A differenza della logica tradizionale (bivalente o "crisp"), che impone di scegliere tra vero o falso, acceso o spento, zero o uno, la logica fuzzy permette di appartenere a più stati contemporaneamente.
Un cibo può essere molto buono, abbastanza buono, mediocre o pessimo, e questi giudizi non si escludono a vicenda. Sono graduali, sovrapposti, contestuali. È così che pensiamo anche noi.
Un cameriere può essere stato “abbastanza gentile”, “non proprio scortese” , e la bandeja paisa può essere “buona” ma “servita tiepida”. Categorie sfumate, parziali, che imitano il modo umano di valutare.
Sistema Fuzzy: dalla percezione soggettiva al numero
Decidere quanta propina lasciare non è una questione puramente numerica.
È un equilibrio tra riconoscenza, fastidio, imbarazzo tra percezione soggettiva e contesto. In questo esperimento ho progettato un sistema fuzzy in stile Mamdani, per simulare il processo decisionale alla base di una semplice domanda: quanto merita questo cameriere? Non voglio essere né tirchio né troppo generoso. Ma il servizio? Il cibo? L’atmosfera? La musica?
Per simulare un giudizio umano, il sistema fuzzy segue un processo in quattro fasi. Ognuna corrisponde a un passaggio fondamentale: dalla percezione soggettiva al numero finale.
| Fase | Cosa fai | Metodo Mamdani |
|---|---|---|
| 🌫️Fuzzificazione | Numeri → gradi fuzzy | triangular_mf(...) |
| 🧠Inferenza | Regole → curve tagliate | min(antecedente, curva output) |
| 🧩 Aggregazione | Unisci le curve | max() punto per punto |
| 🎯Defuzzificazione | Curva → numero | centroide |
🌫️ Fuzzificazione
Nel mondo reale, valutiamo le cose in modo sfumato. Il servizio non è “buono” o “cattivo”: è mediamente buono, o quasi decente.
La fuzzificazione serve proprio a tradurre numeri grezzi in gradi di appartenenza fuzzy.
🧠Inferenza
Ora che sappiamo quanto ogni input “appartiene” a un certo concetto fuzzy, possiamo formulare le regole.Ogni regola è una frase condizionale, del tipo:
Se il servizio è medio e il cibo è medio → la propina sarà media
Se l’atmosfera è piacevole → la propina sarà alta
Se la musica è fastidiosa → la propina sarà bassa
🧩 Aggregazione
A questo punto, ogni regola fuzzy ha generato una curva di propina "tagliata".
Per esempio, se la regola 2 (“se l’atmosfera è piacevole allora la propina è alta”) ha un’attivazione di 0.6, allora la curva fuzzy che rappresenta propina alta viene troncata orizzontalmente a 0.6: non vale più 1, ma “fino a 0.6 di verità”.
🎯 Defuzzificazione
A questo punto abbiamo una curva, ma nel mondo reale serve un numero preciso: il 15%, il 16.2%, il 20%. La fase di defuzzificazione serve proprio a questo: convertire la curva fuzzy aggregata in un singolo numero reale.
📋 Come giudico il pranzo?
Chiunque abbia visto anche solo una puntata di MasterChef conosce il rituale: lo chef concorrente impiatta con precisione chirurgica, cammina verso il banco dei giudici con il fiato sospeso, e resta lì, in silenzio, ad aspettare il verdetto. Poi arrivano loro — i giudici — con lo sguardo critico e il palato allenato, pronti a cogliere ogni dettaglio.
Non basta che il piatto sia buono. Serve equilibrio, tecnica, personalità. Si giudica il gusto, certo, ma anche la presentazione, la coerenza, l’idea dietro al piatto.
Ecco, quando mi viene chiesto di lasciare la propina, mi sento un po’ così: chiamato a dare un voto, a fare il giudice finale.
Così ho iniziato a pensare a quelli che, per me, sarebbero i criteri di valutazione, le variabili soggettive che definiscono la mia esperienza a tavola.
Nel mio sistema fuzzy ne ho scelte quattro: la qualità del servizio, del cibo, dell’atmosfera e — dettaglio tutt’altro che secondario qui in Colombia — il volume della musica. Perché quando la musica è troppo alta, anche il miglior piatto rischia di perdere sapore.
Il mio sistema fuzzy prende in input quattro variabili soggettive, che rappresentano ciò che davvero incide sulla mia esperienza a tavola:
- Qualità del servizio (da 0 a 10)
Intesa come cortesia, disponibilità, attenzione e professionalità del personale. Un cameriere frettoloso o distratto può rovinare anche la cena più buona. - Qualità del cibo (da 0 a 10)
Valutata secondo il gusto personale, e quindi profondamente soggettiva: un piatto può essere tecnicamente ben fatto, ma non incontrare le mie aspettative. - Gradevolezza dell’atmosfera (da 0 a 10)
Comprende luci, arredi, disposizione degli spazi, temperatura e, in generale, la sensazione di comfort e accoglienza che si respira nel locale. - Livello di rumore (volume della musica) (da 0 a 10)
Qui entra in gioco un elemento particolarmente importante in Colombia, dove è comune trovare la musica — spesso reggaetón — a volumi che rendono difficile parlare. Per me, questo ha un impatto diretto sul giudizio complessivo: una cena “urlata” non è mai davvero piacevole.
🔊 Perché il rumore è importante… e il reggaetón ancora di più
In Colombia, è prassi comune trovare la musica ad alto volume praticamente ovunque: nei ristoranti, nei bar, nei supermercati, perfino nelle panetterie di quartiere. E quasi sempre si tratta di reggaetón, presente in loop come sottofondo costante.
Personalmente, trovo questo genere molesto, al punto da non riuscire neppure a considerarlo musica. Quando il volume è alto, la conversazione si interrompe, la convivialità si spezza, e tutto l’ambiente si raffredda. È una forma di disturbo sensoriale che compromette l’esperienza, anche se a livello inconscio.
E non sono l’unico a pensarla così: la Colombia ha recentemente introdotto una legge nazionale contro il rumore che prevede limiti acustici più severi, controlli ambientali più frequenti, e sanzioni economiche importanti per chi li supera.
✍️ Le mie valutazioni
servizio = 6.5 # Il cameriere è stato cortese, ma non impeccabile
cibo = 4 # Cibo decente, ma con margine di miglioramento
atmosfera = 8 # Locale accogliente, ben curato
musica = 3 # Musica un po’ invadenteQuesti numeri non rappresentano verità assolute, ma impressioni soggettive, che il sistema fuzzy trasformerà in un suggerimento percentuale per la propina — un numero che cerca di essere giusto non solo matematicamente, ma anche umanamente.
🌫️Fase 1: Fuzzificazione
In un sistema di logica fuzzy, ogni variabile linguistica (“basso”, “medio”, “alto”, “piacevole”, ecc.) è modellata da una funzione di appartenenza (o "membership functions") che assegna a ogni elemento di un insieme un "grado di appartenenza" (o "grado di verità") compreso tra 0 e 1.
Una delle più comuni è la funzione triangolare, semplice e intuitiva: cresce linearmente da 0 a 1, poi decresce da 1 a 0.
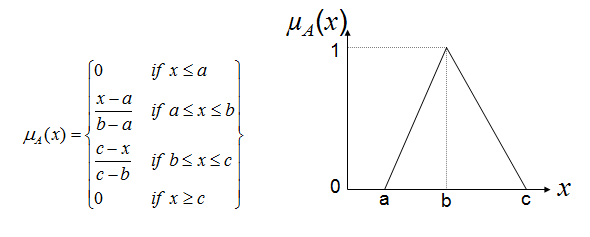
Adesso non ci resta che calcolare i gradi di appartenenza, definendo una funzione che calcola il grado di appartenenza di x a un triangolo fuzzy con vertici a, b, c.
def triangular_mf(x, a, b, c):
"""
Funzione di appartenenza fuzzy triangolare μ_A(x)
con vertici a, b, c dove μ_A(b) = 1 e μ_A(a) = μ_A(c) = 0
"""
x = np.array(x)
y = np.zeros_like(x)
# Lato sinistro del triangolo, parte crescente: (a ≤ x ≤ b)
# μ_A(x) = (x - a) / (b - a)
if b != a:
y = np.where((x >= a) & (x <= b), (x - a) / (b - a), y)
# Lato destro del triangolo, parte decrescente: (b ≤ x ≤ c)
# μ_A(x) = (c - x) / (c - b)
if c != b:
y = np.where((x >= b) & (x <= c), (c - x) / (c - b), y)
# I valori al di fuori di [a, c] sono già inizializzati a 0
return np.clip(y, 0, 1)La funzione triangular_mf restituisce, per ogni valore x, quanto quel valore appartiene a un insieme fuzzy rappresentato da un triangolo definito da tre parametri:
- a = punto iniziale (dove l’appartenenza inizia a salire da 0)
- b = punto centrale (il vertice del triangolo, dove l’appartenenza è massima = 1)
- c = punto finale (dove l’appartenenza torna a 0)
Questa funzione è il cuore di ogni sistema fuzzy basato su regole. Ti permette di trasformare numeri concreti (come “servizio = 6.5”) in gradi di appartenenza fuzzy (“servizio è medio con grado 0.4”), che poi vengono usati nelle regole di inferenza.
Gradi di appartenenza Fuzzy
Dopo aver definito la funzione di appartenenza fuzzy triangolare triangular_mf (che abbiamo visto in precedenza), possiamo finalmente utilizzarla per valutare la realtà con occhi fuzzy.
Il nostro obiettivo è capire, per ciascuna variabile della scena (servizio, cibo, atmosfera, musica), quanto appartiene a una certa categoria linguistica: “medio”, “piacevole”, “fastidiosa”, ecc.
# Gradi fuzzy
s_medio = safe_trimf(servizio, 2.5, 5, 7.5)
c_medio = safe_trimf(cibo, 2.5, 5, 7.5)
a_piacevole = safe_trimf(atmosfera, 5, 10, 10)
m_fastidiosa = safe_trimf(musica, 0, 0, 5)
Quanto il servizio è medio? Usiamo la funzione triangular_mf con un triangolo centrato su b = 5 per rappresentare il concetto di “medio”:
- cresce da 0 a 1 tra 2.5 e 5
- decresce da 1 a 0 tra 5 e 7.5
Se ad esempio servizio = 6.5, il risultato sarà circa 0.40: il servizio è “mediamente medio”.
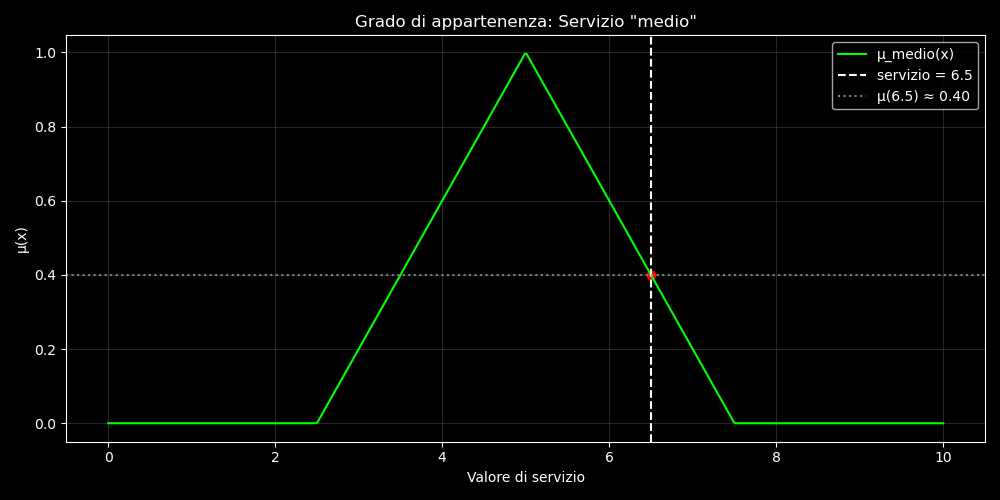
Il grafico mostra in modo chiaro la funzione di appartenenza fuzzy triangolare per il concetto di servizio “medio”.
- Il triangolo è definito da: a=2.5 , b=5, c=7.5
- Il valore osservato è servizio = 6.5
- Il grado di appartenenza calcolato è μ(6.5) ≈ 0.4
- Il punto è evidenziato in rosso, con linee guida verticali e orizzontali.
# Il trinagolo è definito dai parametri
a = 2.5
b = 5
c = 7.5
# valore che vogliamo valutare
x = 6.5
# Sappiamo che è il lato destro del triangolo
# Quindi consideriamo la parte decrescente: (b ≤ x ≤ c)
# μ_A(x) = (c - x) / (c - b)
# Poiché x si trova tra b e c, usiamo la formula del lato destro
if b <= x <= c:
mu = (c - x) / (c - b)
else:
mu = 0 # fuori dal triangolo
print(f"Grado di appartenenza μ({x}) = {mu}")
μ(6.5)=0.4
Una volta compreso come si calcola il grado di appartenenza per la variabile servizio, il procedimento per le altre — cibo, atmosfera, musica — non è affatto diverso. Si tratta sempre di valutare, rispetto a una funzione triangolare, quanto un certo valore ricada dentro un concetto vago come “medio”, “piacevole” o “fastidioso”.
Queste quattro righe di codice calcolano quindi la percezione fuzzy soggettiva delle variabili della nostra scena:
- Quanto il servizio e il cibo possono essere considerati “medi”
- Quanto l’atmosfera risulti “piacevole”
- Quanto la musica sia percepita come “fastidiosa”
Tutti questi gradi di appartenenza — numeri tra 0 e 1 — saranno poi combinati nelle regole del sistema fuzzy, per produrre una decisione finale: quanta propina lasciare, in modo fluido, graduale e realistico. Proprio come farebbe una mente umana.
🧠Fase 2: Regole di inferenza fuzzy
Dopo aver calcolato quanto ogni variabile appartiene a un certo concetto fuzzy — ad esempio, quanto il servizio è “medio” o quanto l’atmosfera è “piacevole” — siamo pronti a formulare delle regole fuzzy di inferenza, molto simili a frasi in linguaggio naturale.
Fu proprio questo il passo decisivo che trasformò la logica fuzzy da teoria matematica astratta a strumento pratico per il controllo e la decisione.
Negli anni ’70, Ebrahim H. Mamdani (1942–2010), ingegnere britannico di origine iraniana, fu il primo a implementare questi concetti in modo sistematico.
Nel 1975 sviluppò un sistema di controllo fuzzy per un piccolo motore a vapore, creando un insieme di regole linguistiche capaci di tradurre l’esperienz di un operatore umano in un sistema logico-formale basato su insiemi fuzzy.
Le regole assomigliavano a questa:
IF la temperatura è alta AND la pressione è bassa
THEN apri la valvola un po’.
Questa struttura — basata su un antecedente e un conseguente — divenne la base di un’intera famiglia di sistemi di inferenza fuzzy:
IF [antecedente]
THEN [conseguente]
Da allora, il metodo di Mamdani è diventato lo standard de facto per molti sistemi fuzzy, specialmente in contesti in cui è fondamentale imitare il ragionamento umano: automazione, domotica, assistenti intelligenti, e naturalmente… calcolo della propina.
Nel nostro esempio, useremo tre regole fuzzy in stile Mamdani, formulate in modo intuitivo e leggibile, proprio come frasi in linguaggio naturale — ma implementate in Python.
regola1 = min(s_medio, c_medio) # → propina media
regola2 = a_piacevole # → propina alta
regola3 = m_fastidiosa # → propina bassaOgni regola collega percezioni sfumate (come “servizio medio” o “musica fastidiosa”) a una possibile propina, secondo una logica umana, ma formalizzata.
Regola 1: servizio medio ∧ cibo medio → propina media
Cominciamo analizzando la prima regola fuzzy, che possiamo esprimere così:
Se il servizio è “medio” e (and) il cibo è “medio”, allora la propina sarà “media”.Formalmente:
servizio medio ∧ cibo medio → propina mediaLa parte a sinistra della freccia è l’antecedente della regola.
Qui compare un AND logico (congiunzione), stiamo cioè verificando quanto sia vera l’affermazione “servizio e cibo sono medi”.
Nella logica classica (booleana) quella che possiamo far risalire ai filosofi Aristotele e Parmenide, la congiunzione AND risponde alla domanda:
È vero che A e B sono entrambi veri?
Con valori booleani (0 o 1), la tabella di verità è semplice:
solo se A = 1 e B = 1, il risultato è 1; in tutti gli altri casi, è 0.
Nel mondo della logica fuzzy, invece, le verità non sono assolute ma sfumate.
Quindi la domanda cambia:
Quanto è vera l’affermazione “servizio e cibo sono medi”?
Come si calcola questa “verità fuzzy”? Utilizzando il metodo Mamdani, interpretiamo l’AND come:
Il grado di verità dell’intera espressione è pari a quanto è vera la meno vera delle due condizioni.
In pratica, usiamo la funzione min():
regola1 = min(s_medio, c_medio)
Ad esempio, se:
s_medio = 0.4 #il servizio è “mediamente medio”
c_medio = 0.6 # il cibo è “abbastanza medio”allora:
regola1 = min(0.4, 0.6) = 0.4
Nel contesto fuzzy, il valore di attivazione della regola è semplicemente il minimo tra i due gradi di appartenenza.
Questo rappresenta quanto riteniamo vera, in modo sfumato, la premessa della regola.
Regola 2: atmosfera piacevole → propina alta
La seconda regola fuzzy è più semplice e lineare rispetto alla prima.
Possiamo esprimerla così:
Se l’atmosfera è “piacevole”, allora la propina sarà “alta”.
Formalmente:
atmosfera piacevole → propina alta
Nel codice:
regola2 = a_piacevole
In questo caso, l’antecedente è composto da una sola condizione, quindi non c’è alcuna congiunzione (AND) da calcolare. Qui il grado di verità dell’antecedente — cioè quanto l’atmosfera è piacevole — coincide direttamente con il grado di attivazione della regola. Ad esempio: se a_piacevole = 0.6, allora la regola 2 sarà attiva con forza 0.6
Regola 3: musica fastidiosa → propina bassa
Anche questa regola è molto diretta:
Se la musica è fastidiosa, allora la propina sarà bassa.
Formalmente:
regola3 = m_fastidiosa
È la stessa struttura della regola precedente: un’unica condizione, quindi il grado di attivazione della regola coincide esattamente con quanto fastidiosa è la musica, secondo la nostra funzione fuzzy.
Se ad esempio:
m_fastidiosa = 0.4
allora:
regola3 = 0.4In questo caso, la fastidiosità della musica agisce come un freno che abbassa la mancia suggerita.
Le tre regole attivate
print(regola1, regola2, regola3
Output: 0.4 0.6 0.4| Regola | Output attivato | Intensità |
|---|---|---|
| Servizio ∧ Cibo medi | propina media |
0.4 |
| Atmosfera piacevole | propina alta |
0.6 |
| Musica fastidiosa | propina bassa |
0.4 |
Questi valori non sono numeri finali, ma interruttori fuzzy che ci dicono quanto ogni regola dovrebbe influenzare l’output.
Nel metodo Mamdani, useremo questi gradi per modulare le curve fuzzy corrispondenti (bassa, media, alta), tagliandole orizzontalmente al livello di attivazione. Questo ci porterà alla prossima fase:👉 l’aggregazione.
🔄 Implicazione fuzzy (taglio delle curve)
Abbiamo ottenuto, per ciascuna regola, un grado di attivazione. Ora dobbiamo trasformarlo in una modifica concreta sulle curve di output associate (le funzioni di appartenenza della propina).
Nel metodo Mamdani, questo passaggio si chiama implicazione fuzzy, e consiste nel:
troncare (tagliare) la curva fuzzy corrispondente a ciascun output, orizzontalmente al livello dell’attivazione.
✂️ Come si fa in pratica?Abbiamo tre funzioni di appartenenza sull’universo della propina, che rappresentano i tre possibili output:
# Insieme universo per l’output: da 0% a 30%
# 500 punti
x_propina = np.linspace(0, 30, 500)
propina_bassa = triangular_mf(x_propina, 0, 0, 15)
propina_media = triangular_mf(x_propina, 10, 15, 20)
propina_alta = triangular_mf(x_propina, 15, 30, 30)
E tre gradi di attivazioni dalle regole:
attivazione_bassa = regola3
attivazione_media = regola1
attivazione_alta = regola2Ora applichiamo il taglio orizzontale (troncamento):
# Troncamento dei grafici (implicazione fuzzy)
output_bassa = np.minimum(attivazione_bassa, propina_bassa)
output_media = np.minimum(attivazione_media, propina_media)
output_alta = np.minimum(attivazione_alta, propina_alta)
Perché facciamo così? Stiamo semplicemente dicendo “voglio solo la porzione della curva fuzzy che non supera questo valore”. Questo è il cuore del metodo Mamdani, ogni regola non genera un numero, ma una curva fuzzy tagliata in base a quanto è attiva.
🧩 Fase 3: Aggregazione delle regole
Abbiamo più regole che propongono diverse conclusioni fuzzy:
- regola1 → propina media → output_media (tronca la curva media)
- regola2 → propina alta → output_alta (tronca la curva alta)
- regola3 → propina bassa → output_bassa (tronca la curva bassa)
Utilizzando il metodo Mamdani,
Ora dobbiamo unite tutte e tre le curve attivate in un'unica curva complessiva, , che rappresenta la propina fuzzy risultante. Nel metodo Mamdani, si usa l’unione (max) tra le curve:
output_aggregato = np.fmax(output_bassa, np.fmax(output_media, output_alta))L’aggregazione non è altro che l’equivalente fuzzy del “sommare i contributi delle regole”.
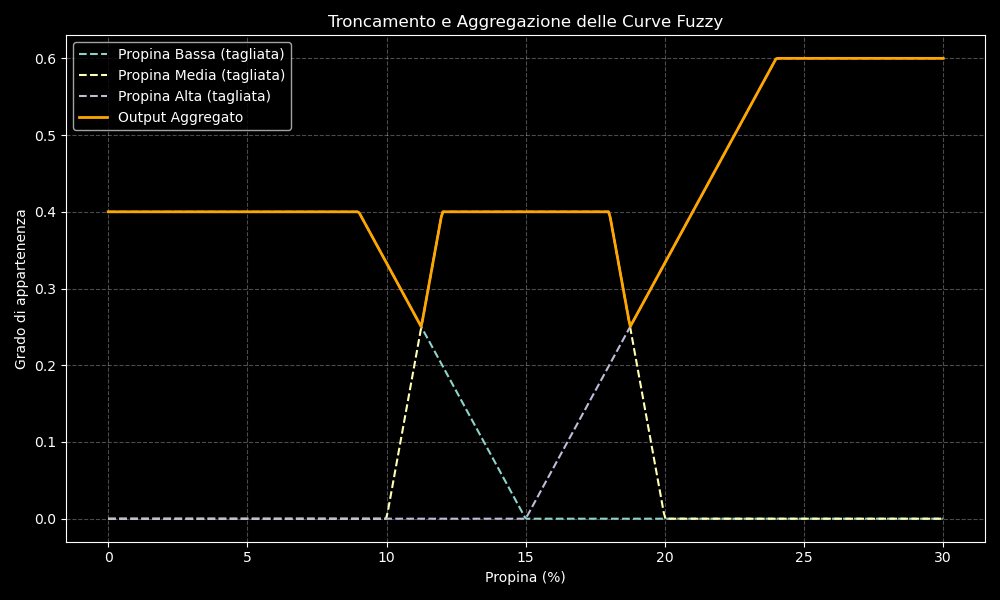
Questo è il grafico che mostra le curve fuzzy tronche (implicazione fuzzy) e la loro aggregazione finale secondo il metodo Mamdani.
Le curve tratteggiate rappresentano le curve originali tagliate in base ai gradi di attivazione delle tre regole: propina bassa (azzurra) tagliata a 0.4, propina Media (gialla) tagliata a 0.4 e propina alta (viola) tagliata a 0.6
La curva in arancione rappresenta l’output aggregato, cioè la massima sovrapposizione tra tutte le regole attivate.
🎯Fase 4 : Defuzzificazione
A questo punto del processo abbiamo ottenuto una curva fuzzy aggregata che rappresenta tutte le possibili propine, ciascuna con il proprio grado di verità. Ma nel mondo reale — quello in cui un cameriere attende il conto — non possiamo lasciare una curva, dobbiamo prendere una decisione concreta: scegliere un solo numero. Per farlo non dobbiamo altro che immaginare di tagliare quella curva in cartone, e trovare il punto esatto sotto cui dovresti mettere il dito per tenerlo in equilibrio perfetto.
Il centroide (o centro di massa) è quel punto lungo l’asse orizzontale (della propina) dove si “equilibrerebbe” la curva fuzzy aggregata se fosse una lastra di metallo sottile.
La formula matematica riflette proprio questo concetto fisico di “momento” e “massa”:
\[\text{Propina finale} = \frac{\sum x_i \cdot \mu(x_i)}{\sum \mu(x_i)}\]
Al numeratore abbiamo la somma pesata dei valori di propina e al denominatore la somma dei pesi, cioè l’area complessiva sotto la curva. In Python, possiamo implementarlo così:
# Calcolo del centroide (defuzzificazione)
numeratore = np.sum(x_propina * output_aggregato)
denominatore = np.sum(output_aggregato)
propina_finale = numeratore / denominatore if denominatore != 0 else 0
Questo ci restituisce un valore crisp, cioè un numero unico, chiaro e utilizzabile nella realtà.
print(f"Propina finale suggerita: {propina_finale:.2f}%")
# Output: Propina finale suggerita: 16.27%
Per concludere, possiamo rappresentare tutto con un grafico che chiude il ciclo fuzzy ed interrompe il mio monologo interiore in slow motion
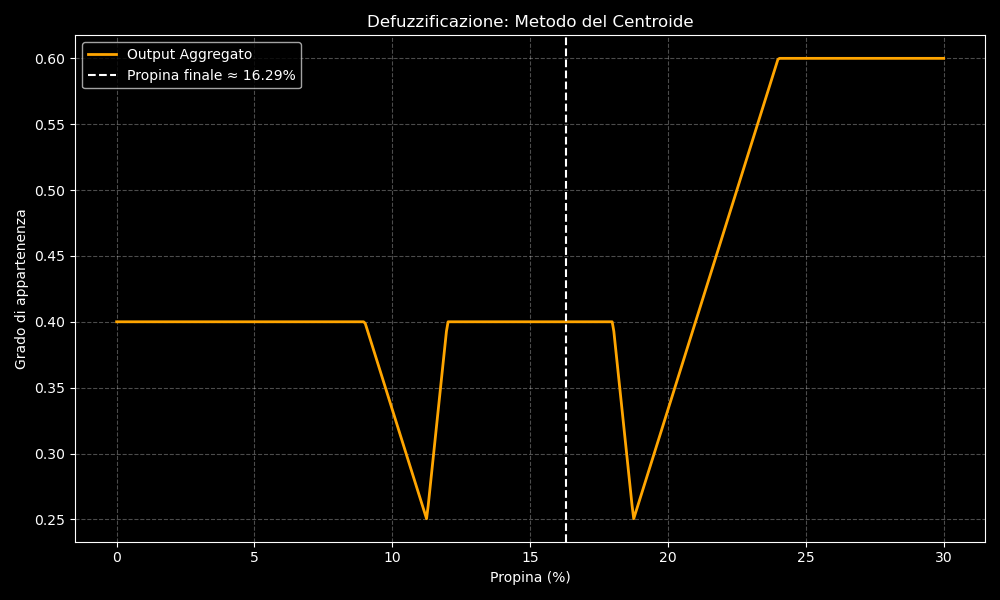
In arancione la curva fuzzy aggregata risultato della sovrapposizione delle regole attivate. Infine la linea tratteggiata bianca, che indica la propina finale calcolata tramite il centroide.
Alla fine quanto dovrei lasciare di propina?
Alla luce del mio giudizio personale — un servizio decente, un cibo passabile, un’atmosfera gradevole e una musica un po’ fastidiosa — il sistema fuzzy suggerisce una propina per il cameriere di circa 16.29%.
Un numero che non nasce da una formula rigida, ma da un equilibrio morbido tra riconoscimento e fastidio, tra merito e disturbo.
Una decisione più umana, meno binaria.
Eppure, la propina non è solo una cifra.
È una forma simbolica di relazione sociale.
In Colombia è volontaria, ma spesso suggerita con insistenza. In altri paesi è obbligatoria, altrove è addirittura considerata scortese.
Dare o non dare una mancia è anche una questione di potere, riconoscimento, contesto.
Può premiare, ma anche discriminare.
Può diventare un dovere morale o una forma di colpa mascherata.
E sempre, inevitabilmente, dice qualcosa su di noi.
Forse la logica fuzzy non risolverà l’ambiguità della propina.
Ma può mostrarcela meglio.
Può ricordarci che anche una macchina, se progettata con sensibilità, può imparare a ragionare come noi:
con misura, incertezza, e un pizzico di buon senso.
Alla fine, forse, il vero problema non è se la propina debba essere inclusa nel conto,
né se l’intelligenza artificiale sia in grado di calcolarla con precisione.
Il vero nodo è riconoscere che dietro ogni propina si nasconde una relazione umana.
E che nessun algoritmo, per quanto avanzato, potrà mai comprenderla del tutto.
Ma potrà almeno imparare a rispettarla.
📚Bibliografia
[0] B. Kosko, Il fuzzy pensiero. Teoria e applicazione della logica fuzzy, Baldini & Castoldi 1999 Milano.
[1] A. G. Pizzaleo, Fuzzy logic. Come insegnare alle macchine a ragionare,
Castelvecchi 2000 Roma
[2] S. Cammarata, Sistemi a logica fuzzy. Come rendere intelligenti le macchine , Etaslibri 1997 Milano,
