It came as a bomb 💣
- John Robinson Pierce

Nel luglio del 1948, a soli 32 anni, il giovane matematico e ingegnere Claude Shannon (1916-2001) pubblicò sul Bell System Technical Journal il celebre articolo A Mathematical Theory of Communication, in cui proponeva un modello statistico del linguaggio basato sugli n-grams e sui canali rumorosi. Per l’ingegnere John Robinson Pierce (1910-2002), che aveva assistito alla nascita del transistor (Fenomenologia del circuito integrato, 2012), il lavoro di Shannon fu “come una bomba 💣 a scoppio ritardato”.

La traduzione come crittografia

Nel 1947, durante un viaggio in treno, il matematico Warren Weaver (1894-1978) lesse l’articolo di Claude Shannon sulla teoria matematica della comunicazione e ne fu profondamente colpito.

Gli venne allora un’intuizione destinata a segnare la storia della traduzione automatica:

la traduzione potrebbe essere un problema di decifrazione

Negli anni successivi collaborò strettamente con Shannon e, nel 1949, pubblicò una versione divulgativa della teoria dell’informazione. In essa mostrava come l’analisi delle frequenze di lettere e combinazioni potesse essere applicata a qualunque lingua, indipendentemente dalla comprensione del suo lessico.

Weaver si rese conto che le lingue, pur nella loro diversità, condividono regolarità statistiche. Persino senza conoscere la lingua sorgente, è possibile dedurre elementi della struttura di un testo osservando la distribuzione delle lettere, la frequenza dei bigrammi e altri indizi formali. In questa prospettiva, la traduzione — o almeno la sua fase iniziale di decodifica — poteva essere concepita come un problema di trasmissione di informazione, più vicino alla crittografia che alla comprensione linguistica in senso stretto.

Che cosa è l’informazione?

L’idea di Shannon era di misurare la quantità di informazione presente in un messaggio emessa da una sorgente, ma che cosa s’intendeva esattamente per misurare l’informazione? Shannon voleva lasciare da parte i fattori psicologici come il significato e concentrarsi solo su quelli fisici del messaggio:

Questi aspetti semantici della comunicazione sono irrilevanti per il problema ingegneristico.

anche se come afferma Weaver non si trattava di una visione ristretta della comunicazione, ma che comprende:

non solo il linguaggio scritto e orale, ma anche la musica, le arti pittoriche, il teatro, il balletto e di fatto tutto il comportamento umano

Proviamo ora ad immaginare  il ricevente come una persona che è incerta su quale tra i  messaggi possibili prodotti e trasmessi dalla sorgente riceverà.

L’aspetto significante è che l’effettivo messaggio sia uno selezionato da un insieme di messaggi possibili.

Così facendo,  un messaggio diventa la quantità di informazione che fa passare il ricevente da uno stato di incertezza ad uno di ordine (o di minor incertezza).
L’intuizione di Shannon fu quella di riconoscere un’analogia fra l’idea d’informazione e quella di entropia equiparando lo stato di incertezza associato ad un messaggio e il disordine della meccanica statistica.

La mia più grande preoccupazione era come chiamarla. Pensavo di chiamarla informazione, ma la parola era fin troppo usata, così decisi di chiamarla incertezza.

Fu il matematico John Von Neumann (1903-1957) a suggerire a Shannon di adottare il termine entropia per indicare il valore medio dell’informazione disponibile alla sorgente.

Quando discussi della cosa con John Von Neumann, lui ebbe un’idea migliore. Mi disse che avrei dovuto chiamarla entropia, per due motivi: ‘Innanzitutto, la tua funzione d’incertezza è già nota nella meccanica statistica con quel nome. In secondo luogo, e più significativamente, nessuno sa cosa sia con certezza l’entropia, così in una discussione sarai sempre in vantaggio

Il consiglio venne accolto da Shannon anche perché era consapevole che il termine infomazione nella sua teoria evidenziava una inaspettata analogia tra due contesti così distanti tra loro come la nascente teoria dell’informazione e la termodinamica.

La sua formula dell'entropia è:

\[H(X)= -\sum_{x} p(x) \log_2 p(x)\]

esprime l’incertezza media associata a un messaggio. Se tutte le lettere hanno la stessa probabilità di comparire, l’entropia raggiunge il suo valore massimo; se invece una lettera domina (ad esempio la e), l’entropia diminuisce. Questo concetto è fondamentale per stimare quanta informazione è contenuta in un testo.

John von Neumann osservò che la formula chiave della teoria dell’informazione ricalca un risultato già ottenuto nel 1877 dal fisico Ludwig Boltzmann (1844-1906), nel caso particolare in cui tutti gli stati siano equiprobabili:

\[S = k \log W\]

Il legame tra le due espressioni è profondo: entrambe misurano il grado di incertezza su uno stato del sistema, ma in ambiti diversi. Shannon quantifica l’informazione in bit, mentre Boltzmann misura l’entropia termodinamica in joule per kelvin, una grandezza fisica legata al disordine microscopico.

Alice🐇nel paese delle meraviglie

L’interesse di Warren Weaver per la traduzione andava ben oltre l’ambito tecnico. Era infatti affascinato da "Alice nel paese delle meraviglie" di Lewis Carroll, pseudonimo del matematico Charles Lutwidge Dodgson (1832-1898), opera nota per i suoi giochi linguistici e i paradossi logici — come quelli presenti nella celebre scena del tè del Cappellaio Matto.

Weaver arrivò a collezionare 160 edizioni di Alice in 42 lingue diverse, proponendo un metodo comparativo per valutare la qualità delle traduzioni, focalizzandosi su passaggi particolarmente complessi come i giochi di parole e le rime.

Nel 1964 pubblicò l'opera "Alice in Many Tongues", un libro in cui analizzava le difficoltà legate alla traduzione del testo di Carroll, corredato da una bibliografia basata sulla propria collezione personale. Per questo progetto, Weaver collaborò con figure di spicco come l’antropologa Margaret Mead, che valutò la traduzione in pidgin del Pacifico, il sindaco di Gerusalemme tra il 1965-1993 Teddy Kollek (1911-2007) , e il biochimico Hugo Theorell (1903-1982) , per la traduzione in svedese.

L'entropia di Alice🐇

Per il nostro esperimento useremo come testo di riferimento Alice’s Adventures in Wonderland , nella versione di pubblico dominio disponibile su Project Gutenberg.
Il primo passo è scaricare il file in formato Plain Text UTF-8 e leggerlo in una variabile. Subito dopo, eseguiamo una pulizia di base: convertiamo tutto in minuscolo, rimuoviamo caratteri diversi dalle lettere a–z e dagli spazi, e sostituiamo sequenze di spazi con un singolo spazio.

# 1) Scarica Alice in Wonderland (Plain Text UTF-8)
URL = "https://www.gutenberg.org/files/11/11-0.txt"
txt = requests.get(URL, timeout=30).text

# 2) Pulisci: minuscole, solo lettere a–z e spazi
txt_clean = txt.lower()
txt_clean = re.sub(r"[^a-z\s]+", " ", txt_clean)
txt_clean = re.sub(r"\s+", " ", txt_clean).strip()

Questo ci garantisce un testo omogeneo, pronto per l’analisi delle frequenze di lettere e per il calcolo dell’entropia.

Adesso per calcolare l’entropia è necessario stimare la distribuzione di probabilità delle lettere presenti in un testo. Nel nostro esperimento considereremo solo le 26 lettere dell’alfabeto inglese e se tutte avessero la stessa probabilità di comparire, l’entropia raggiungerebbe il valore massimo teorico:

\[log_{2} 26 \approx 4.7004 \ \text{bit/simbolo}\]

Quindi nessun testo scritto con queste 26 lettere può avere un’entropia maggiore.

A questo punto il passo successivo consiste nel calcolare la distribuzione di probabilità delle lettere in Alice in Wonderland e, a partire da essa, determinare l’entropia secondo la formula di Shannon.

alfabeto = "abcdefghijklmnopqrstuvwxyz"


# 3) Funzioni per frequenze ed entropia (Shannon)
def frequenze_lettere(testo):
    """
    Restituisce la frequenza relativa di ogni lettera.
    """
    conteggi = Counter(c for c in testo if c in alfabeto)
    totale = sum(conteggi.values())
    return {l: conteggi.get(l, 0) / totale for l in alfabeto}

def entropia_testo(testo):
    """
    Calcola l'entropia H(X) di un testo.
    """
    freq = frequenze_lettere(testo)
    return -sum(p * math.log2(p) for p in freq.values() if p > 0)

# Calcolo dell'entropia di Alice
random.seed(42)  # per replicabilità
H_alice = entropia_testo(txt_clean)
print("Entropia di Alice in Wonderland:", H_alice)

L’entropia di Alice’s Adventures in Wonderland è pari a \(H \approx 4.1615 \\{bit/simbolo}\), ben al di sotto del massimo teorico di \(log_{2} 26 \approx 4.7004 \ \text{bit/simbolo}\)

Entropia di Alice in Wonderland: 4.161492370069989

Questo scarto riflette la ridondanza dell’inglese scritto, dove alcune lettere come e, t, a, o compaiono molto più spesso di altre. La distribuzione non uniforme rende il testo più prevedibile rispetto a un insieme di lettere perfettamente equiprobabili.

Simulazione di un canale rumoroso

Shannon immaginava la comunicazione come un flusso di simboli che attraversa un canale soggetto a interferenze: durante il percorso, una parte del messaggio può essere corrotta o alterata.
Per visualizzare questo concetto, simuliamo un canale rumoroso in cui ogni lettera ha una probabilità di errore ε di essere sostituita con un’altra scelta a caso (mentre gli spazi rimangono invariati).

#4) Canale rumoroso: con probabilità ε sostituisce la lettera con un’altra a caso
def canale_rumoroso(testo, errore=0.2):
    out = []
    for ch in testo:
        if ch in alfabeto and random.random() < errore:
            out.append(random.choice(alfabeto))
        else:
            out.append(ch)
    return "".join(out)


for eps in [0.0, 0.1, 0.2, 0.3, 0.4]:
    rumoroso = canale_rumoroso(txt_clean, errore=eps)
    H_noisy = entropia_testo(rumoroso)
    print(f"epsilon={eps:.1f} | H Alice={H_alice:.4f} | H rumoroso={H_noisy:.4f}")

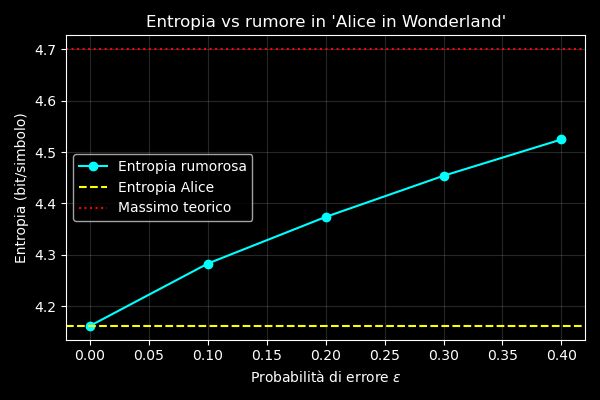
Variando ε possiamo osservare come il rumore influisca sull’entropia del testo: all’aumentare del rumore, la distribuzione delle lettere tende a uniformarsi e l’entropia si avvicina al valore massimo teorico di \(log_{2} 26 \approx 4.7004 \ \text{bit/simbolo}\)

Entropia di Alice in Wonderland: 4.161492370069989
epsilon=0.0 | H Alice=4.1615 | H rumoroso=4.1615
epsilon=0.1 | H Alice=4.1615 | H rumoroso=4.2840
epsilon=0.2 | H Alice=4.1615 | H rumoroso=4.3760
epsilon=0.3 | H Alice=4.1615 | H rumoroso=4.4552
epsilon=0.4 | H Alice=4.1615 | H rumoroso=4.5194

Il grafico mostra come l’entropia di Alice’s Adventures in Wonderland aumenti progressivamente all’aumentare della probabilità di errore ε nel canale di trasmissione.

Decodifica probabilistica

Un canale rumoroso non distrugge necessariamente l’informazione, infatti se conosciamo la distribuzione di probabilità della sorgente, possiamo tentare di ricostruire il messaggio più probabile anche dopo che il canale ha introdotto errori.

def decodifica_probabilistica(messaggio_rumoroso, frequenze_note):
    """
    Mappa le lettere del messaggio rumoroso a quelle più probabili
    secondo le frequenze attese (approccio semplificato).
    """
    freq_rumoroso = frequenze_lettere(messaggio_rumoroso)
    ordine_rumoroso = sorted(freq_rumoroso, key=freq_rumoroso.get, reverse=True)
    ordine_attese = sorted(frequenze_note, key=frequenze_note.get, reverse=True)
    mappa = dict(zip(ordine_rumoroso, ordine_attese))
    return "".join(mappa.get(ch, ch) for ch in messaggio_rumoroso)

Nel nostro esempio non mostriamo l’output decodificato per intero perché il testo di Alice’s Adventures in Wonderland è molto lungo. Utilizziamo invece le prime ~300 lettere, in modo da mantenere l’output leggibile e concentrarci sul comportamento della decodifica probabilistica.

Conoscendo la distribuzione di probabilità delle lettere nella lingua di partenza (qui calcolata sul testo di Alice), possiamo tentare di correggere il messaggio ricevuto da un canale rumoroso sostituendo le lettere più “sospette” con quelle più probabili.

# Frequenze attese dal testo originale di Alice
freq_attese_alice = frequenze_lettere(txt_clean)

# Creiamo un messaggio rumoroso
estratto_alice = txt_clean[:300]
random.seed(42)
msg_rum = canale_rumoroso(estratto_alice, errore=0.3)

# Decodifica semplice
msg_decod = decodifica_probabilistica(msg_rum, freq_attese_alice)

print("Messaggio originale:", estratto_alice[:30] + "...")
print("Messaggio rumoroso:", msg_rum[:30] + "...")
print("Messaggio decodificato (grezzo):", msg_decod[:30] + "...")

Come si vede, il testo decodificato non coincide con l’originale: il nostro algoritmo considera solo le frequenze globali delle lettere, ignorando il contesto e la sequenza.

Entropia di Alice in Wonderland: 4.161492370069989
Messaggio originale: start of the project gutenberg...
Messaggio rumoroso: siert on cqe projeat nuyedbebg...
Messaggio decodificato (grezzo): woean ri lqe carvetn idjeusesb...

Per ricostruzioni più accurate, occorrerebbero modelli probabilistici più sofisticati, come bigrammi, trigrammi o reti neurali.

Capacità del canale

Shannon dimostrò che la quantità massima di informazione che può passare attraverso un canale rumoroso è:

\[C=H(X)−H(X∣Y)\]

dove \(H(X)\) è l’entropia dell’input e \(H(X∣Y)\) rappresenta l’incertezza residua sull’input una volta osservato l’output corrotto dal rumore.
Nel nostro esperimento non calcoliamo esplicitamente \(H(X∣Y)\), ma il concetto resta chiaro: più il rumore è intenso, più cresce l’incertezza residua e minore sarà la capacità del canale.
Questo significa che, anche conoscendo le statistiche della lingua, esiste un limite fisico oltre il quale nessuna strategia di decodifica potrà recuperare il messaggio originale.

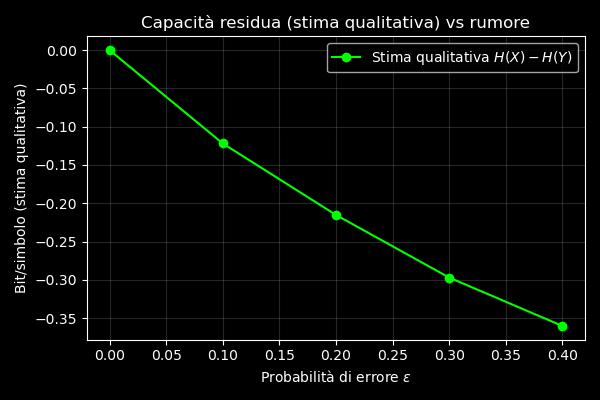
La curva verde lime mostra \(H(X)−H(X∣Y)\) ovvero una stima qualitativa della capacità residua del canale. Quando ε=0, la capacità è massima poiché il testo ricevuto coincide perfettamente con quello originale. All’aumentare del rumore, invece, la capacità crolla rapidamente verso lo zero, riducendo drasticamente la quantità di informazione originale ancora recuperabile.

Il potere dell'intuizione

Abbiamo visto che, anche senza conoscere il significato di un messaggio, è possibile ricostruirne la probabile struttura sfruttando le regolarità statistiche. Questo è il cuore dell’intuizione di Warren Weaver:

“Anche se non si sa quale lingua sia stata codificata, le frequenze delle lettere, delle combinazioni e dei pattern possono guidare la decifrazione.”

Weaver, in fondo, non stava solo studiando il linguaggio naturale, ma lo trattava come un sistema codificato, in cui l’informazione può essere modellata, compressa, predetta e corretta. È un paradigma che attraversa tutta la linguistica computazionale e che, dal telegrafo ai modelli transformer di oggi, non ha mai perso attualità.

In un ambito apparentemente distante, ma sorprendentemente affine, lo psicanalista Carl Gustav Jung (1875-1961) — nel suo Tipi psicologici (1921) — definiva l’intuizione come "la percezione inconscia di una realtà che non è ancora entrata nella sfera della coscienza". Per Jung, l’intuizione è una funzione psichica capace di cogliere schemi, connessioni e possibilità prima che la ragione li renda espliciti.

Quello che Shannon formalizzò con la teoria dell’informazione e Weaver applicò al linguaggio, Jung lo descriveva nella dinamica della mente: riconoscere un ordine nascosto prima che sia visibile, captare il segnale sotto il rumore.

Ed è forse qui che risiede il vero “potere dell’intuizione”: la capacità di intravedere il messaggio ancora prima di poterlo leggere.