Immaginate un cane che intento ad inseguire una lepre si ritrovi davanti ad un trivio e debba decidere quale percorso abbia scelto la sua preda.
Questo aneddoto attribuito al filosofo Crisippo (281 - 204 a.C.) , che verrà ripreso e reso famoso quasi cinque secoli dopo da Sesto Empirico , serviva a dimostrare come il cane avesse fatto un ragionamento di questo tipo:

la preda è passata o di qua o di là o per quell'altra parte. Per di qua non per di là no, dunque per quell'altra parte

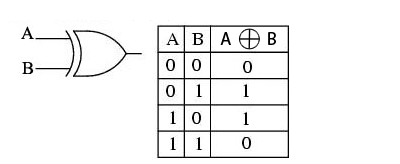
Questo per gli stoici sarebbe un esempio di ragionamento detto del "quinto indimostrabile" ossia la dimostrazione della regola della disgiunzione esclusiva (XOR) che risulta vera solo se uno dei disgiunti è vero , (1+0=1;0+1=1) dunque escludendo che lo siano entrambi (0+0=0; 1+1=0).
Crisippo la formulava come “quello che da un collegamento disgiuntivo e dal contrario di una delle parti collegate conclude l'altra” , cioè “o è giorno o è notte, ma non è notte. Dunque è giorno” (Sesto empirico, Schizzi Pirroniani).

Questi ragionamenti “non hanno bisogno di dimostrazione perché, nel caso loro, risulta di per sé abbastanza evidente la loro conclusione” (Sesto Empirico, Contro i logici).

I limiti del perceptron
Nel 1957 lo psicologo Frank Rosenblatt fornì una prima formalizzazione della nozione di apprendimento in una rete neurale a singolo strato  inteso come modifica dei pesi (weights) e in un scondo articolo nel 1962  “Principles of neurodynamics”.
La funzione di trasferimento delle unità di output è quella a soglia detta anche di Heaviside ed è definita da

Il perceptron venne discusso criticamente da Marvin Minsky e Seymour Papert nel libro “Perceptrons: an introduction to Computational Geometry” del 1969 dimostrando che la classe di funzioni che era in grado di discriminare era limitata alle forme linearmente separabili.
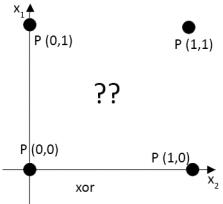
Se posizioniamo i dati in un sistema cartesiano notiamo il perceptron non riuscirebbe ad apprendere questo problema semplicemente perché non esiste una superficie di decisione tale da separare con una linea retta gli input dagli output.

La ridotta capacità computazionale del perceptron determinò una perdita di interesse sull'argomento per  più di 10 anni ponendo fine a ciò che il matematico Douglas Hofstadter, autore di “Godel, Escher e Bach”, aveva definito come l'età dell'oro del sogno booleano dell'intelligenza artificiale. Fu solo attraverso lo sviluppo delle reti multistrato (MLP) e dell'algoritmo di retro-propagazione dell'errore (EBP), introdotto dal connessionismo nel 1986 ,che si riaccese l'interesse per le reti neurali artificiali.

Bibliografia
[1] Sesto Empirico: Schizzi pirroniani, II, Roma-Bari, Laterza, 1988
[2] D. Parisi, Intervista sulle reti neurali, Il Mulino, 1989
[3] G. Carrella ,L'officina neurale. Viaggio tra la teoria e la pratica delle reti neurali, FrancoAngeli,1995
[4] D. Floreano, Manuale sulle reti neurali, il Mulino, 1996
[5] S. Cammarata,Reti neuronali, dal perceptron alle reti caotiche e neuro-fuzzy, Etas,1997