“L’ultima cosa che si decide quando si scrive un libro” ,osservava il filosofo Blaise Pascal (1623-1662) , “è che cosa mettere all’inizio”.
Così ho deciso d’iniziare questo tutorial sui tools di MATLAB per la logica fuzzy con il classico problema sul come dare la mancia al ristorante: dato un numero fra 0 e 10 che rappresenti la qualità del servizio al ristorante (dove 10 è eccellente) ed un altro numero sempre fra 0 e 10 per la qualità del cibo.
Di quanto dovrebbe essere la mancia?
Sfruttando l’approccio fuzzy riusciamo a ridurre il gap esistente tra persone e macchine definendo il problema nel nostro linguaggio naturale lasciando così alla macchina il compito di tradurre tali operazioni.
Impostiamo un set di regole Fuzzy
Per definire un insieme di regole fuzzy, occorre stabilire innanzitutto il numero di regole ed i valori fuzzy da associare alle variabili di input e di ouput. Infine creare le associazioni di input-output per ogni regola. Iniziamo con scrivendo un primo set di regole legate al servizio e a quanta mancia dovremmo dare:
|
1 2 3 |
1. Se il servizio è scadente, allora la mancia sarà bassa 2. Se il servizio è buono, allora la mancia sarà media 3. Se il servizio è ottimo, allora la mancia sarà elevata |
Ora dobbiamo includere quanto incide la qualità del cibo sulla mancia, possiamo aggiungere le due seguenti regole:
|
1 2 |
4. Se il cibo è rancido, allora la mancia sarà bassa 5. Se il cibo è buono, allora la mancia sarà |
A questo punto combiniamo i due set di regole per ottenerne uno solo:
|
1 2 3 |
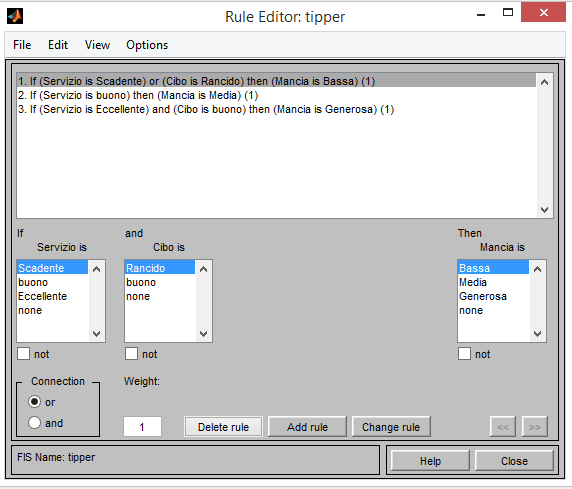
1. Se il servizio è scadente o il cibo è rancido, allora la mancia sarà bassa. 2. Se il servizio è buono, allora la mancia sarà media. 3. Se il servizio è eccellente o il cibo è buono, allora la mancia sarà generosa. |
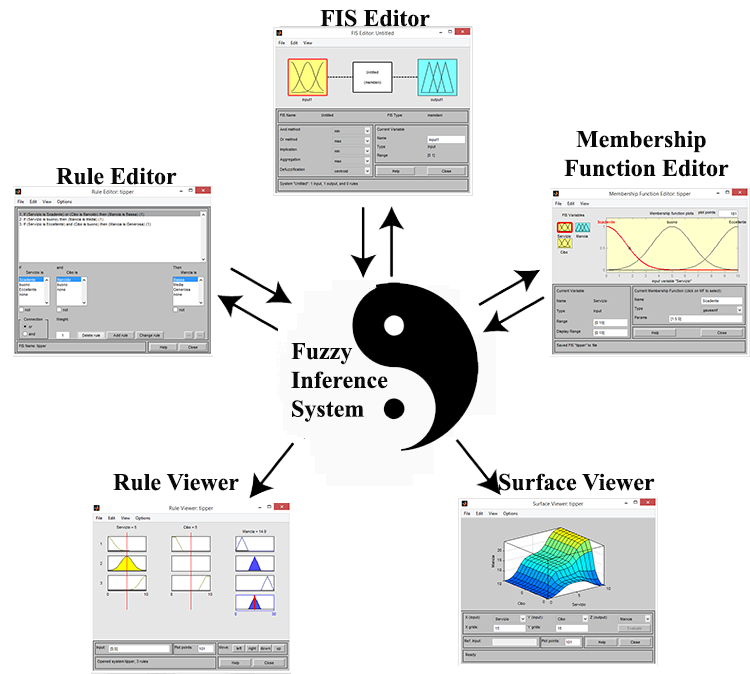
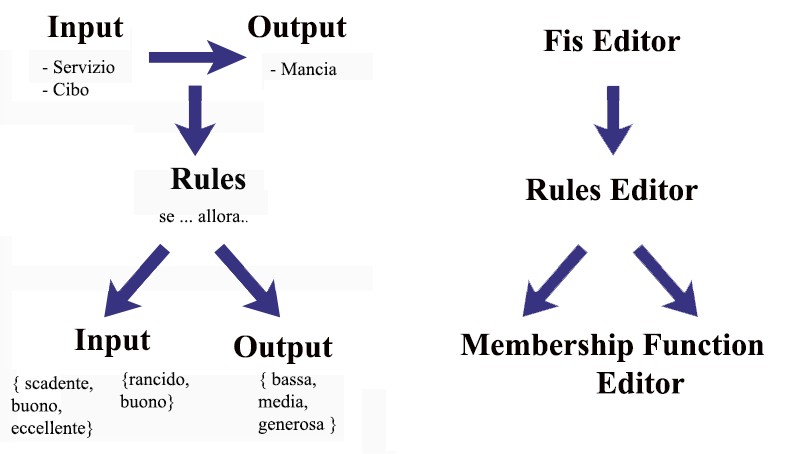
Schematizzando il problema che affronteremo con i Fuzzy Logic Toolbox di MATLAB avremmo quindi due input Servizio e Cibo, tre regole ed un solo output Mancia.
Utilizzeremo FIS editor per specificare quante e quali variabili di input/output e MF editor per specificarne stati e funzioni d’appartenenza.Infine utilizzeremo Rule editor per specificare le regole if-then invece per analizzare i dati Rule e Surface editors.
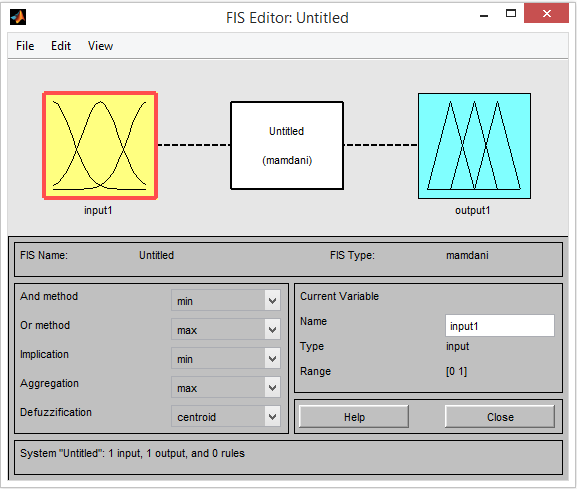
FIS editor
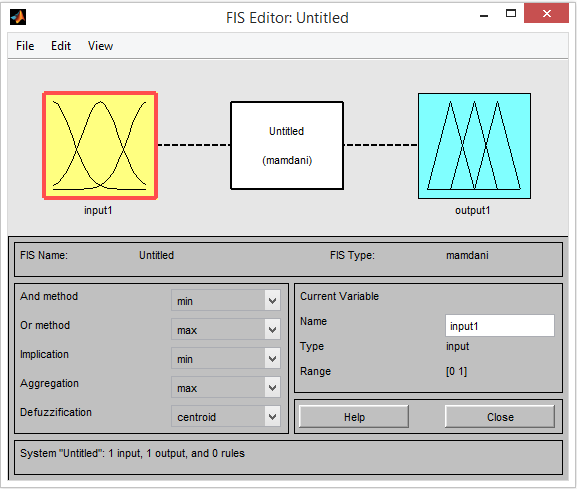
Per iniziare digitiamo fuzzy nel prompt di MATLAB così facendo si aprirà una sessione di FIS editor con un solo input con l’etichetta “input1” ed un output con “output1”.
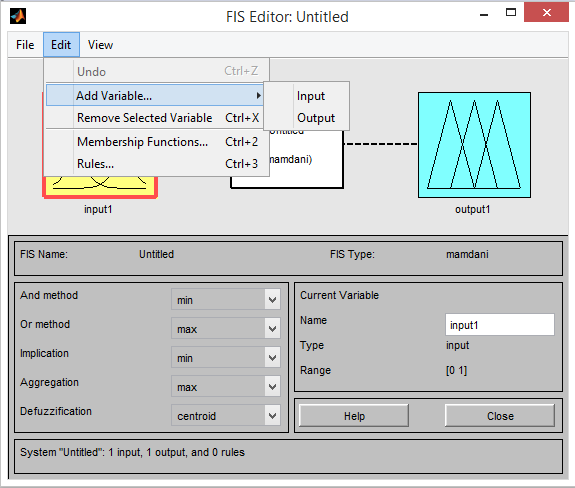
Per il nostro esempio costruiremo un sistema fuzzy con due inputs ed un solo output quindi come prima cosa andremo alla voce Edit del menu e selezioneremo Add Variabile ed infine Input. Comparirà così un seconda variabile con l’etichetta Input2.
I due inputs che andremo a definire saranno quindi le variabili linguistiche Servizio e Cibo e l’unico output sarà la variabile Mancia.
Definire input e output
Come primo input avremmo la variabile linguistica Servizio che avrà un universo del discorso da 1 a 10 con i termini primari: scadente, buono , eccellente. Ed ognuno con la propria funzione d’appartenenza . Invece come secondo input avremmo la variabile Cibo con un universo da 1 a 10 ed i termini: rancido, buono e relative funzioni d’appartenenza. Infine la variabile di output Mancia avrà l’universo con il valore da 5% a 25% con i termini: minima, media, generosa ognuno con la propria funzione d’apparteneza.
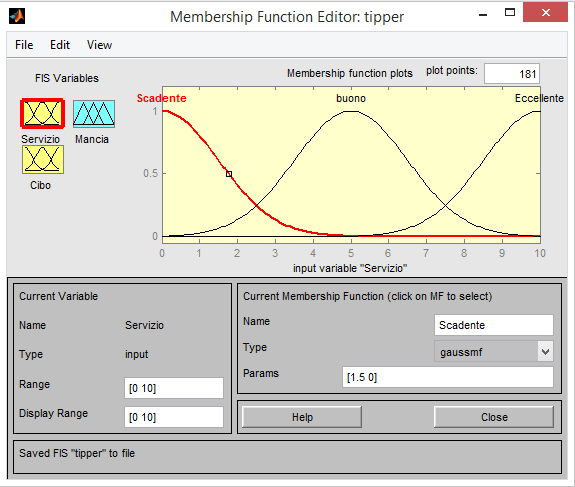
Membership Function Editor
Il matematico Lofti Zadeh afferma che le variabili fuzzy possono essere considerate come delle variabili linguistiche i cui valori non sono numeri ma parole o frasi espresse in un linguaggio naturale o artificiale.
Le variabili di input (Servizio, Cibo,mancia) e di output sono quindi variabili linguistiche suddivise cioè in un insieme di termini che coprano il loro intero universo del discorso. Ad esempio per Servizio avremmo:scadente,buono ed eccellente con le relative funzioni d’appartenenza.
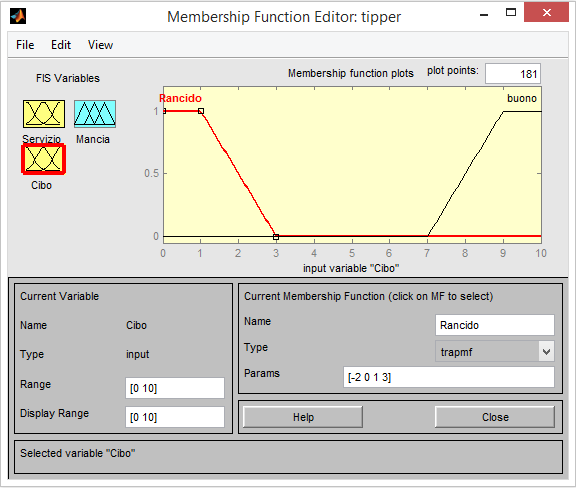
Per la variabile linguistica Cibo avremmo i termini primari :rancido e buono.
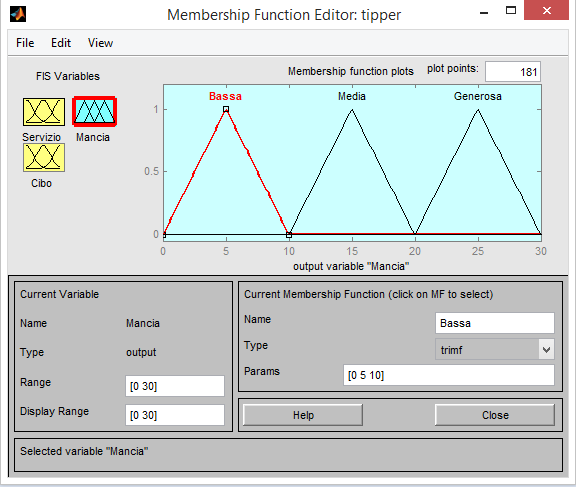
Infine come variabile di output avremmo Mancia con i termini: bassa, mediaa e generosa.
Rule editor
Nel 1974 in Gran Bretagna l’ingegnere Ebrahim H. Mamdani e Seto Assilan realizzarono il primo il primo sistema di controllo di un generatore a vapore basato sulla logica fuzzy e nel 1982 solo Madmani invece quello di una fornace per la produzione di cemento. Invece nel 1987 venne realizzato un sistema automatizzato della Hitachi con solo 54 regole fuzzy per il controllo della frenatura dei treni della metropolitana della città di Sendai.
Regole d’inferenza
Mediante le regole IF-THEN otteniamo un sistema fuzzy d’inferenza (Fuzzy Inference System) che realizza un mapping fra input ed output.
Una regola linguistica del tipo If-Then è composta da un antecedente e da un conseguente:
|
1 |
IF (antecedente) THEN (conseguente) |
Dove l’antecedente non è altro che una proposizione fuzzy del tipo (X is A) e il conseguente (Y is B) dove A e B sono i termini primari a cui sono associati gli insiemi fuzzy e le relative funzioni di appartenenza, definiti sugli intervalli di X e Y.
|
1 2 |
IF ( X is A ) THEN ( Y is B ) IF (servizio is scadente) THEN (mancia is bassa) |
Inoltre più proposizioni possono essere collegate fra loro attraverso i connettivi AND, OR, NOT nel nostro esempio infatti abbiamo:
|
1 |
IF (servizio is scadente) OR (cibo is rancido) THEN (mancia is bassa) |
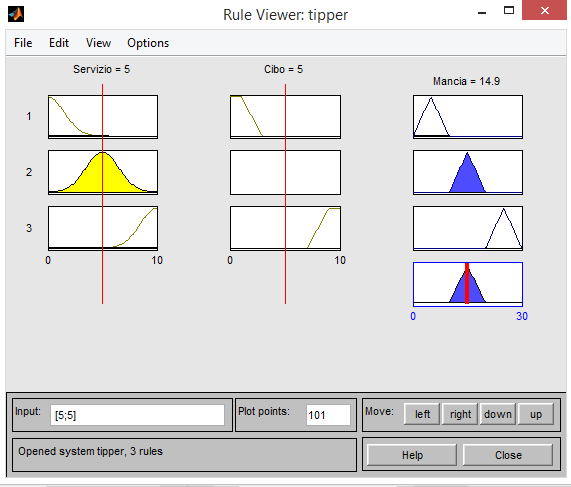
Rule viewer
Le prime due colonne rappresentano le funzioni d’appartenenza degli antecedenti per ognuna delle tre regole d’inferenza invece la terza colonna mostra quelle dei conseguenti. Come ultimo plot della 3 colonna abbiamo invece la fusione dei risultati delle tre regole e la costruzione di un valore finale di percentuale per la mancia che dovremmo dare al ristorante.
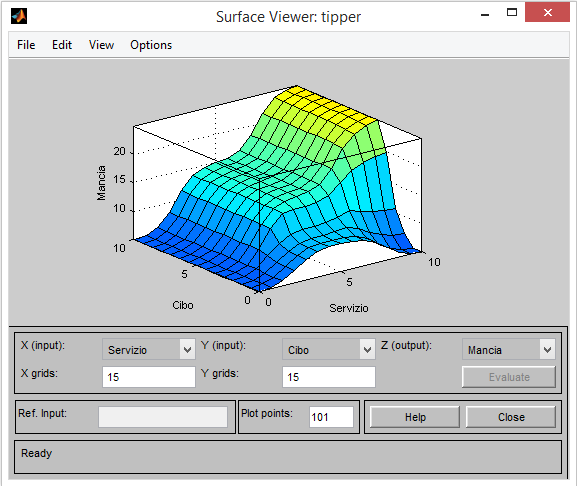
Surface viewer
Sitografia
Bibliografia
[1] B. Kosko,Il fuzzy pensiero. Teoria e applicazione della logica fuzzy, Baldini & Castoldi 1999 Milano.
[2] A. G. Pizzaleo,Fuzzy logic. Come insegnare alle macchine a ragionare,
Castelvecchi 2000 Roma
[3] S. Cammarata,Sistemi a logica fuzzy. Come rendere intelligenti le macchine , Etaslibri 1997 Milano